直列回路の計算は小学校や中学校の理科で習う基本的な知識ですよね。
しかし、基本的な知識であるからこそ、しっかりと理解をしておく必要があります。
今回は直列回路の電圧・電流・抵抗の計算の仕方や考え方などについて解説します。
直列回路とは?

直列回路というのは、電線や抵抗など回路にあるものを全て一直線に接続をした回路のことです。
回路が途中で枝分かれしないため、シンプルでわかりやすいです。

しかし、回路のどこかで断線などがあると全く機能しなくなるといったデメリットもあります。
直列回路はバッテリーや乾電池などの電源回路によく使用されることがあります。
例えば、直列回路で40Vの電圧を出力できるようにしたい場合、1個4Vの電池を10個直列に接続すれば、40Vの電圧を出力することができます。
これは、直列回路全体の電圧は各箇所の電圧の合計に等しくなるという性質を利用したものです。
このように、直列回路は私たちの身の周りで重要な役割を果たしています。
電圧の求め方について

上の記事でも少しお話しましたが、直列回路全体の電圧は回路の各箇所で発生する電圧の合計(和)になります。
なぜ、直列回路では各箇所の電圧の合計が回路全体の電圧に等しくなるのでしょうか?
電圧というのは電流を流そうとする力のことをいいます。そのため電圧が高い程、電流が沢山流れます。
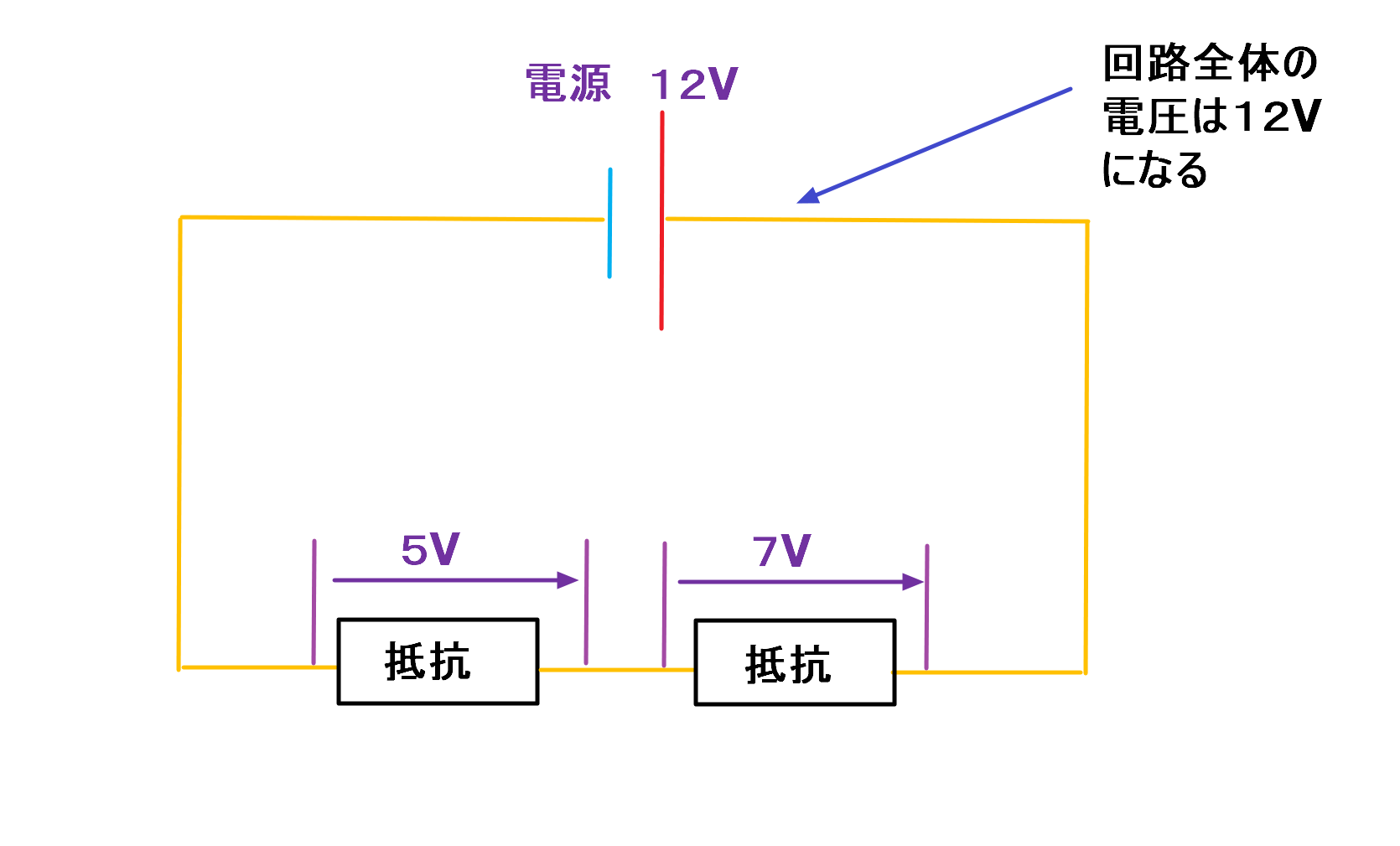
しかし電圧は、抵抗に加わる度にエネルギーとして消費され弱くなっていきます。
直列回路は一直線の回路であることから、抵抗に加わる度に弱くなっていきますが、それらを全て合計すると回路全体の電圧になるということです。
電圧はオームの法則で求めることもでき、$$電圧(V)=電流(A)\times抵抗(Ω)$$で求めることができます。
電流の求め方について

続いて、直列回路の電流の特徴についてですが、電流は回路内のどこで測定しても同じになります。
1箇所の電流が分かれば、回路全体の電流も分かります。
なぜ、直列回路の電流はどこで測定しても同じになるのでしょうか?それは電流の正体を分かっていると理解しやすいです。

電流の正体は単位時間あたりの電子の移動現象です。
世の中のすべての物質は原子で構成されており、その原子の周りを周っているものが電子というものです。
電子は-の電気エネルギーを持っており、外部からエネルギーなどを受け取ると移動することがあります。
この移動が電流と呼ばれているのですが、直列回路は回路の途中で枝分かれなどしないため、電子の数も変わることがありません。
そのため、電子の移動現象である電流は、直列回路のどこで測定しても同じ数値となります。
オームの法則で電流を計算して求める場合は、$$電流(A)=\frac{電圧(V)}{抵抗(Ω)}$$で求めることができます。
抵抗の求め方について

直列回路の全体の抵抗は各箇所の抵抗値の合計(和)が回路全体の抵抗値となります。
なぜ、直列回路全体の抵抗は各抵抗の合計(和)に等しいのでしょうか?
抵抗というのは、電流の流れにくさを表すものです。
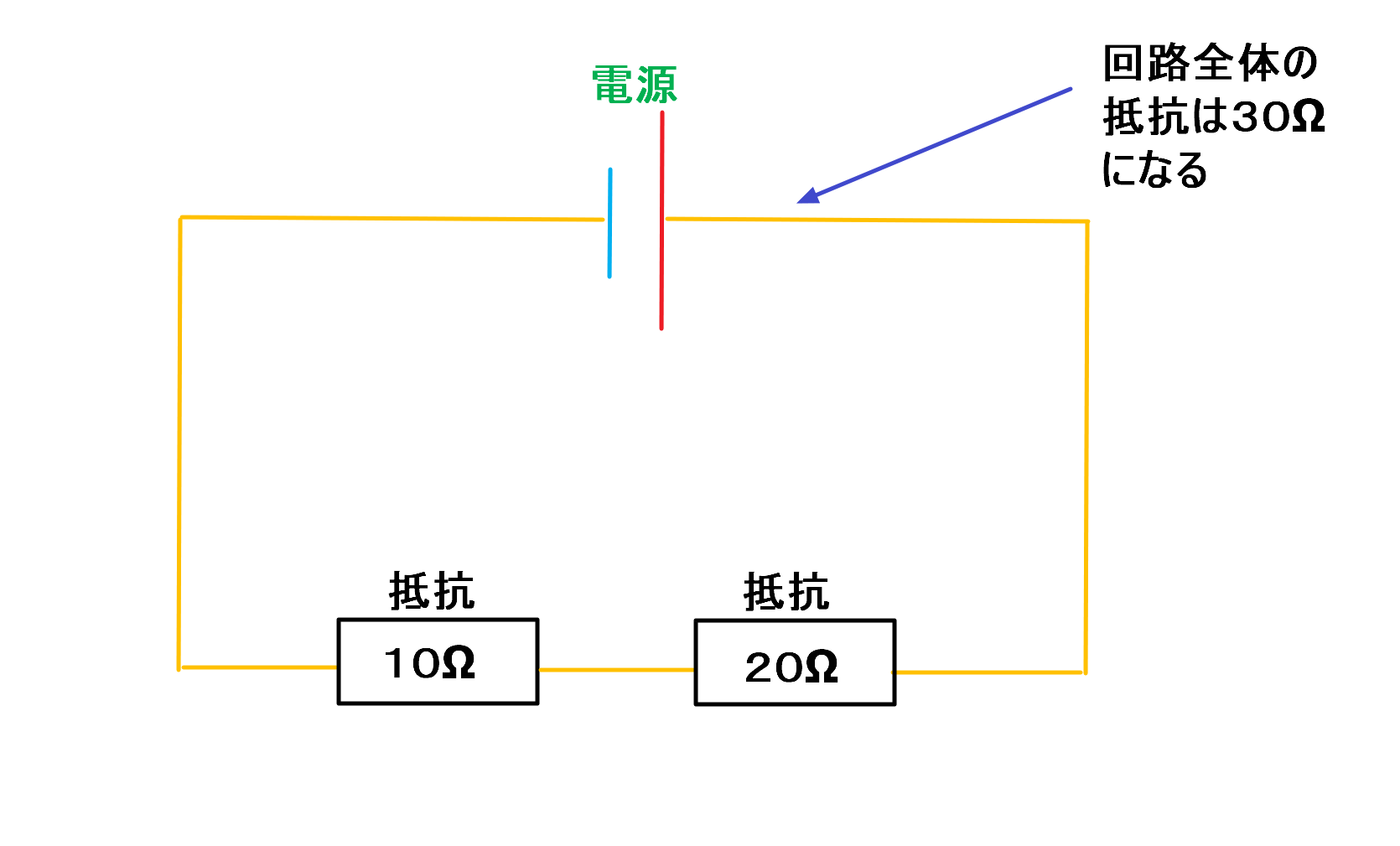
電流の気分になってみた時、回路に抵抗が2つ直列に並んでいたら、2個分の抵抗を通らないといけないのか、、と思いませんか?
直列回路では、並んでいる抵抗を全て通る必要があるため、回路全体の抵抗=各抵抗の合計となります。
オームの法則で抵抗を計算して求める場合は、$$抵抗(Ω)=\frac{電圧(V)}{電流(A)}$$で求めることができます。
直列回路の例題について

これらのことを踏まえて実際に直列回路の計算をしてみましょう。
下の図のような抵抗1と抵抗2を直列に接続した回路があります。
電源電圧が100V、電流が0.5A、抵抗2の電圧が40Vであった場合、抵抗1、抵抗2の抵抗はいくらでしょうか?
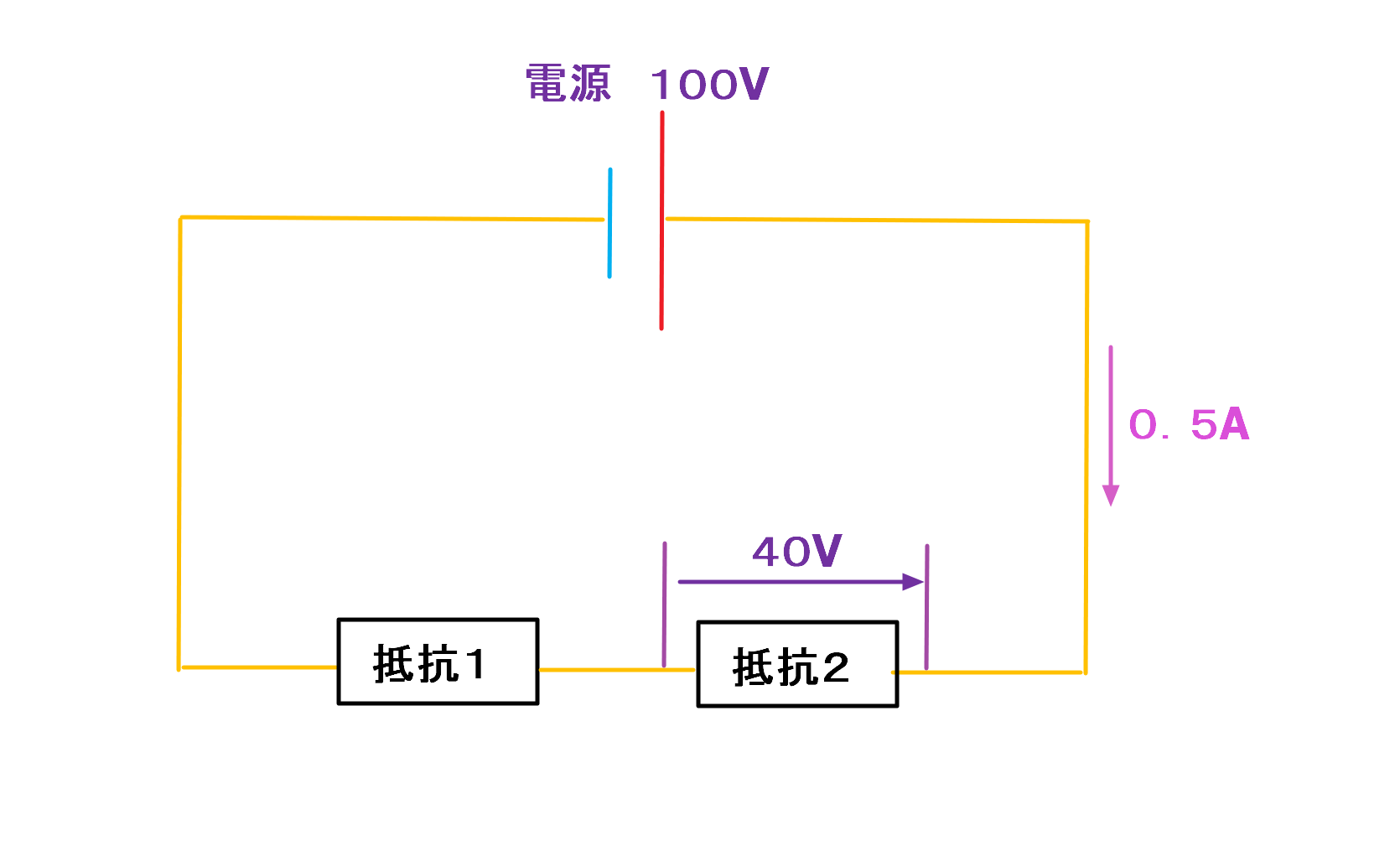
まずは抵抗の求め方を思い出しましょう。
抵抗は$$抵抗(Ω)=\frac{電圧(V)}{電流(A)}$$で求めることができます。
また、直列回路ではどこでも同じ電流が流れ、抵抗2には40Vの電圧が発生していることから、
$$抵抗2(Ω)=\frac{40(V)}{0.5(A)}=80(Ω)$$となります。
次は抵抗1です。まずは抵抗1の電圧を求めます。直列回路の全体の電圧は各箇所の電圧の合計になるため、
抵抗1の電圧は60Vとなります。抵抗1の電流は同じく0.5Aです。よって、
$$抵抗1(Ω)=\frac{60(V)}{0.5(A)}=120(Ω)$$となります。
答えとしては抵抗1が120(Ω)、抵抗2が80(Ω)となります。
以上が抵抗1と抵抗2の求め方です。
今回は抵抗を求めましたが、このように直列回路の性質を利用すれば、電圧や電流も同じく計算で求めることができます。
まとめ
・直列回路は全てのものを一直線に接続した回路のこと
・直列回路の電圧は各箇所の電圧の合計(和)=回路全体の電圧となる
・直列回路の電流はどこで測定しても同じになる
・直列回路の抵抗は各箇所の抵抗の合計(和)=回路全体の合計となる
いかがだったでしょうか?
以上が直列回路の特徴についてまとめたものです。
中学校の理科でも習いますが、なぜこのような特徴があるのか理由までは詳しく知らない方が多いと思います。
また、下記の記事では並列回路の計算方法や電圧とはどのようなものなのかということを詳しく解説してますので、併せて是非読んでみてください。








コメントを残す