私たちが普段使用する機器や家電にはコンデンサが利用されています。
コンデンサには様々な性質があり、とても便利であることから多くの機械に使用されています。
その性質の中でも、コンデンサの特徴の基本とも言えるものに、容量リアクタンスというものがあります。
今回の記事ではコンデンサの容量リアクタンスとは一体何なのか、どのようにして求めることができるのかについて解説していきます。
コンデンサとは

まずは、そもそもコンデンサがどのようなものなのか簡単に解説します。
コンデンサとは2つの導体(金属類)の間に絶縁体(ゴムや空気など)を挿入しているものです。

導体の間に絶縁体を挿入することにより、2つの導体に電荷を蓄えることができるようになります。
電荷とは+や-などの電気量をもった粒子のことで、電流や電圧を発生させるものです。
この電荷を蓄える性質を利用し、異常な電圧が発生した時には吸収させたり、必要な時だけ蓄えた電荷を放電させるなどしてよく使用されます。
以上がコンデンサの簡単な概要となります。
容量リアクタンスとは

コンデンサには上記でお話した電荷を蓄える性質の他に、電流の流れを妨げる性質があります。
この電流を妨げる性質は抵抗と同じように働くと考えることができ、コンデンサの抵抗という意味合いで容量リアクタンスと呼ばれています。
容量リアクタンスは記号として表す時はXc、単位は抵抗と同じくΩが使用されています。
なぜ、コンデンサには抵抗と同じように電流を妨げる働きがあるのかというと、上記でお話した電荷を蓄える性質があるためです。
例えば、下の図のようにコンデンサのみ接続した交流の回路があったとします。
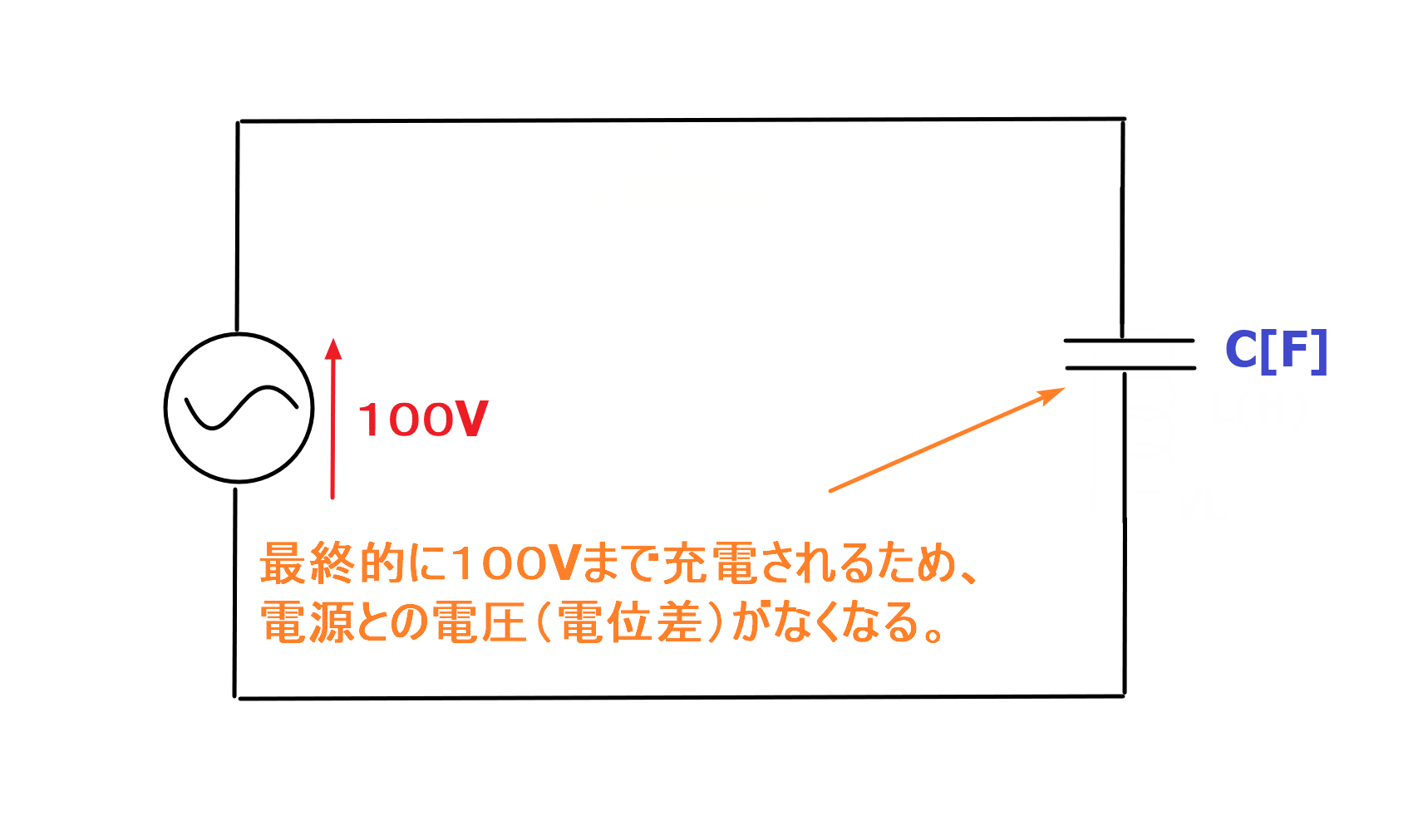
時間の経過とともにコンデンサは電源から充電されることになります。
電源が100Vのため、最終的にはコンデンサも最大で100Vまで充電されます。
コンデンサが100V、電源が100Vになるということはコンデンサと電源間の電圧(電位差)は0Vになります。
電圧が0Vになれば、電流も流れなくなってしまいます。
そのため、コンデンサの充電する性質は電流を流さなくなる要因となっています。
以上が容量リアクタンスの概要とメカニズムです。
容量リアクタンスに流れる電流の位相について

コンデンサ(容量リアクタンス)にはもう一つの特徴があります。
交流回路にコンデンサを接続すると電流の位相が電圧の位相より90°進むことになります。
なぜ、電流の位相が90°進むのかというと、これもコンデンサの電荷を蓄える性質が関係しています。
コンデンサは電荷を蓄えるため、最終的には電源と同じ電位になるまで充電されます。
電源と同じ電位になると、回路に電圧(電位差)がなくなるため、電流が流れなくなります。
このことを踏まえてコンデンサが接続された回路の電圧と電流の波形を見てみると、なぜ電流の位相が電圧よりも90°進むことになるのかがわかります。

上の波形はコンデンサを接続した時の交流回路の電圧と電流の波形です。
電圧の波形が最大の時①(コンデンサが電源と同電位の時)は電位差がないため、電流は0になってしまいます。
また、電圧の波形が0の時②は電源との電圧(電位差)が大きいため、電流は最大の大きさとなります。
そのため、電圧の大きさと電流の大きさの変化にズレが生じ、90°の位相差が発生します。
これがコンデンサを接続した時に電流の位相が90°進む理由です。
容量リアクタンスの求め方について

容量リアクタンスは下記の計算式で求めることができます。
$$Xc=\frac{1}{ωC}=\frac{1}{2πfc}[Ω]$$
なぜこのような計算式になるのかというと、コンデンサは電荷を蓄える性質があるため、静電容量Cと電圧・電流の関係からこの式を導き出しているからです。
静電容量Cというのは、コンデンサがどれくらい電荷を蓄えることができるのかを示す値のことです。
例えば、下の図のような静電容量がC(F)のコンデンサのみ接続された交流回路があったとします。
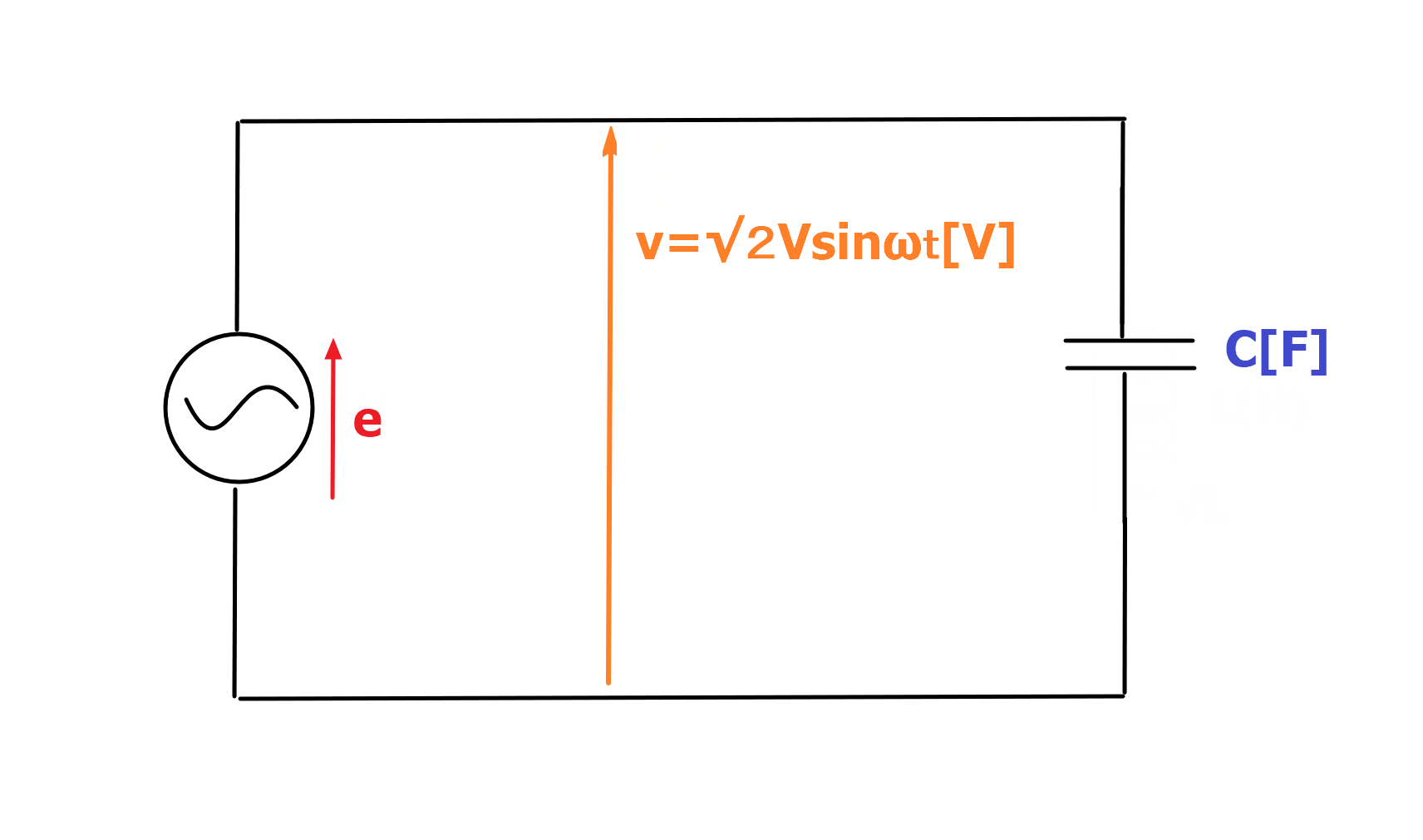
静電容量Cと電荷qには下記のような関係があります。
$$q=CV[C]$$
そのため、コンデンサに蓄えられる電荷は、
$$q=Cv=√2VCsinωt[C]$$
と表せます。
また、電流iは時間あたりに移動する電荷の量であることから、電流iは下のように表すことができます。
$$i=\frac{Δq}{Δt}=C\frac{Δv}{Δt}=C\frac{Δ√2Vsinωt}{Δt}[A]$$
さらにこの式を時間tで微積すると、
$$i=C\frac{Δv}{Δt}=C\frac{dv}{dt}(√2Vsinωt)[A]$$
$$i=√2ωCVcosωt[A]$$
$$i=√2ωCVsin(ωt+\frac{π}{2})[A]$$
となり、上の式のiは瞬時値であり、ωCVというのは式の形から電流の実効値Iと等しくなることがわかります。
このことから、実効値とωCVの関係を整理すると、
$$I=ωCV=\frac{V}{\frac{1}{ωC}}[A]$$
となり、分母である1/ωCはオームの法則でいう抵抗Rとみなすことができます。
これが一番最初にお話した式で容量リアクタンスを求められる理由になります。
そして、容量リアクタンスXcは静電容量Cと周波数fが大きい程、小さな値となります。
以上が、容量リアクタンスXcの求め方と式の解説です。
まとめ
・コンデンサには電荷を蓄える性質があり、充電されることで電流が流れにくくなる。この流れにくさを容量リアクタンス(Xc)という。
・容量リアクタンス(Xc)は1/ωCで求めることができる。
・コンデンサを接続すると、電流の位相は電圧の位相よりも90°進む。
今回は容量リアクタンスの性質、求め方についての説明でした。
コンデンサの性質や容量リアクタンスの考え方は電気知識の基本的な部分となりまので是非参考にしてみてください。
また、今回記事で紹介した容量リアクタンスの他にも誘導リアクタンスという電流を妨げるものもあります。
誘導リアクタンスついては下記の記事で詳細を説明していますので、併せて是非読んでみてください。








コメントを残す