電検の勉強をしていると、相互インダクタンスを求める問題があります。
しかし、解き方だけが分かっていても、今自分は一体何を求めたのだろう、、となりませんか?
難しいイメージがありますが、要点を一つ一つ理解していけば、きちんと理解することができます。
今回は相互インダクタンスの概要、求め方について解説していきます。
相互誘導作用とは

電気の世界には相互誘導作用というものがあります。
具体的にはどのようなものなのかというと、下のように2つの回路があったとします。
回路1に電流が流れた時、回路1にはアンペアの右ねじの法則により磁束1が発生します。
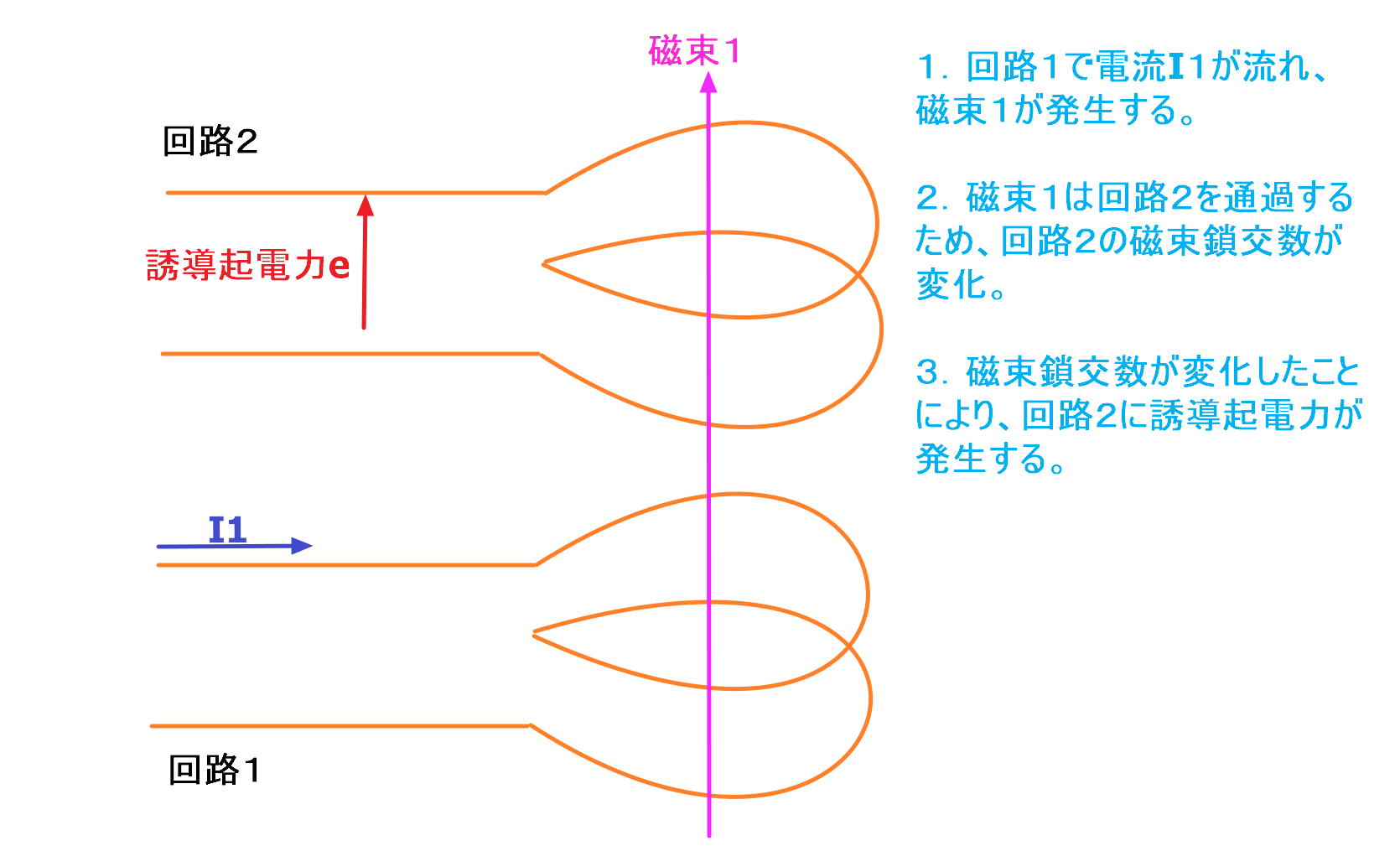
この時に発生した磁束1は、回路2に鎖交するように発生します。
回路2は回路1から磁束1が鎖交してきたことから、回路2の磁束鎖交数が変化します。
回路2の磁束鎖交数が変化すると、レンツの法則により、変化した磁束鎖交数を打ち消すように回路2に誘導起電力が発生します。
このように他の回路の影響で、磁束鎖交数が変化し、誘導起電力が発生する現象を相互誘導作用といいます。
磁束鎖交数、誘導起電力について分からない方は以下の記事を参考にして下さい。
つまり、電流が流れていないはずの回路でも、近くに電流が流れている回路がある場合は、相互誘導作用により電流が流れている可能性があります。
そのため、電流が流れていない回路に触る場合でも、事前に電流、電圧が無いことを確認をしてから触るようにすることが大事です。
以上が相互誘導作用の概要です。
相互インダクタンスとは

上の記事で、相互誘導作用は他の回路の磁束の影響を受けることで磁束鎖交数が変化し、誘導起電力が発生する現象とお話しました。
相互インダクタンスというのは、2つの回路の間で相互誘導作用が起きた時に、どれくらい誘導起電力が発生する関係性なのか、というのを分かるようにしたものです。
なぜそのようなものが必要なのかというと、使用している回路によって、相互誘導作用が起きた時に発生する誘導起電力が変わってくるからです。
例えば、回路に使用している物質や使用しているコイルの大きさ、巻数などによっても誘導起電力の発生の仕方は変わってきます。
他の回路から磁束の変化を受けた時に、どれ程の誘導起電力を発生する回路なのか、回路ごとの性質をわかるようにしたものが相互インダクタンスです。
相互インダクタンスの求め方について

相互インダクタンスは一般的に量記号にM、単位にはH(ヘンリー)が使用されます。
また、相互インダクタンスは計算で求めることができます。
そのためにまずは、電磁誘導によって発生する誘導起電力の求め方を説明します。
下の図で、コイル1の電流をI1、磁束をφ1、巻数をN1、コイル2の誘導起電力をe2、巻数をN2、コイル1の磁束の変化をΔφ1、時間の変化をΔtとします。
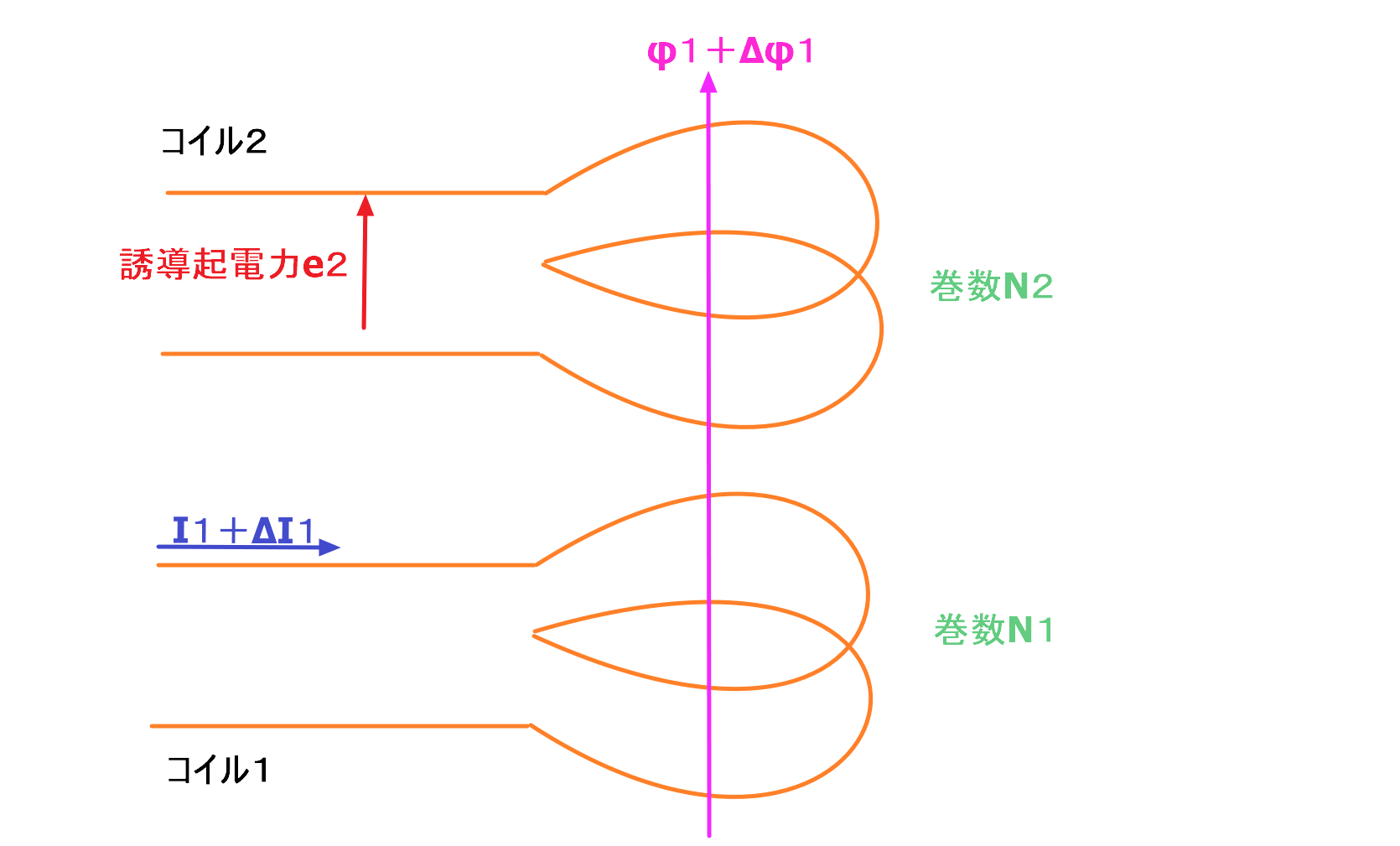
そうすると、コイル2に発生する誘導起電力e2は次の式で求めることができます。
$$e_2=-N_2\frac{Δφ_1}{Δt}(V)$$
もしも透磁率(磁気の通りやすさ)が一定であるなら、磁束は電流の変化に比例します。
そのため、相互インダクタンスM(相互誘導作用による誘導起電力の発生のしやすさ)の関係は下のようになります。
$$e_2=-N_2\frac{Δφ_1}{Δt}=-M\frac{ΔI_1}{Δt}(V)・・・①$$
式を変形すると、$$M=\frac{N_2Δφ_1}{ΔI_1}(H)・・・②$$となります。
式②から、相互インダクタンスは、一方の回路に1Aの電流を流した時、もう一方の回路の磁束鎖交数に等しくなることがわかります。
また、式①からは相互インダクタンスは、一方の回路の電流が毎秒1A変化していると、もう一方の回路に発生する誘導起電力と等しくなることもわかります。
そして、コイル1に流れる電流の変化に対して、コイル2の磁束鎖交数が比例する(両方とも同じ割合で増える)のであれば、
$$M=\frac{N_2φ_1}{I_1}(H)$$で求めることができます。
以上が、相互インダクタンスの求め方です。
相互インダクタンスを求めてみよう(例題)

ここまでの内容を踏まえて、実際に例題を解いてみましょう。
下の図のような2つの円筒コイルにおいて、コイル1は巻数が300、コイル2は巻数が200であったとします。
コイル1に4Aの電流を流した時、発生した磁束がコイル2に鎖交し0.02Wbであった時、コイルの相互インダクタスはいくらになるでしょうか?

上の記事でお話した式をさっそく使ってみましょう。
相互インダクタンスは$$M=\frac{N_2φ_1}{I_1}(H)$$で求めることができます。
上の図から、コイル1の電流は4A、コイル2の巻数は200、コイル2に鎖交した磁束は0.02Wbであることがわかります。
これらを式にあてはめると、$$M=\frac{200\times0.02}{4}=1(H)$$となります。
また、コイルの相互インダクタンスが1Hであることから、コイル1に流れる電流が1秒おきに変化している場合は、コイル1の電流変化とコイル2に発生する誘導起電力は等しくなる関係であることがわかります。
まとめ
・相互誘導作用とは他の回路から磁束の変化受け、誘導起電力が発生する現象
・相互インダクタンスとは相互誘導作用が起きた時、どれ程の誘導起電力を発生する回路なのか、性質をわかるようにしたもの
・相互インダクタンスは$$M=\frac{N_2φ_1}{I_1}(H)$$で求めることができ、量記号にM、単位にはH(ヘンリー)が使用される
いかがだったでしょうか?
相互インダクタンスは難しいイメージがありますが、一つ一つ理解していけば、きちんと理解することができます。
電気の勉強で大切なのは覚えることよりも、理解することです。一度理解したことは忘れにくいものです。
また、電気の世界には自己インダクタンスや電磁誘導という相互インダクタンスに似た現象もあります。
以下の記事では自己インダクタンスや、電磁誘導を利用した変圧器などについても詳しく解説しています。
あわせて是非読んでみてください。










コメントを残す