
並列回路の計算式が分数になる理由には、オームの法則が関係していますよ。
中学の理科や電気系資格の勉強の際に、上記のような疑問を感じることが多いと思います。
今回の記事では、並列回路の計算の仕方や計算式の考え方などについてわかりやすく解説していきます。
並列回路とは

まず、並列回路というのは回路が複数に枝分かれしている回路のことをいいます。
回路が枝分かれしていることから、1本の通り道が断線しても、もう1本の通り道があるため安定性があります。

並列回路は家のコンセント、照明の回路や受電設備など多くの場所で使用されています。
並列回路の電圧について

並列回路の電圧の特徴はどこで測定しても同じ電圧になる点です。
例えば、下の図のような電源が100Vの回路があった場合、どこで測定しても電圧は100Vになります。
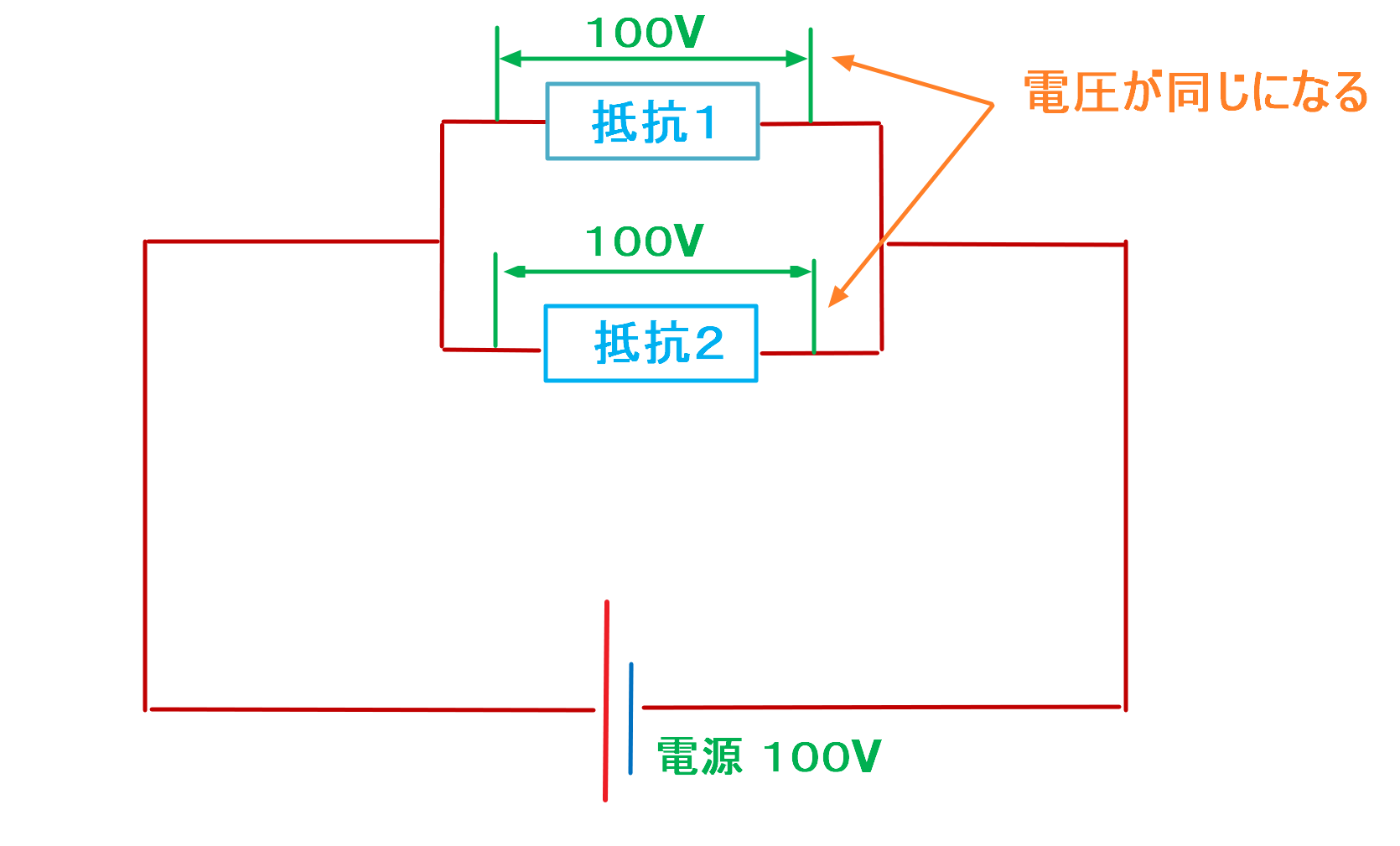
電圧というのは抵抗に電圧が発生するたびにエネルギーとして消費され下がってしまいます。
このような現象は電圧降下と呼ばれています。
電圧降下については、以下の記事で詳細を解説していますので、気になる方は参考にしてください。
しかし、上記のような並列回路の場合は電源から抵抗に電圧がかかるまで電線しかありません。
厳密にいいますと電線内部にも抵抗はありますが、ほぼ0に近い程小さな抵抗のため今回は無視します。
抵抗1と抵抗2に電圧がかかるタイミングは同じです。
そのため抵抗1、抵抗2にかかる電圧は同じ電圧になります。
また、電源の電圧がわからなくても、抵抗、電流がわかっていればオームの法則により計算して求めることもできます。
$$電圧(V)=電流(A)\times抵抗(Ω)$$で求めることができます。

直列回路の場合は、抵抗が一直線に並んでいるから、それぞれの抵抗の電圧が違くなるの?

そうですね!抵抗の大きさにもよりますが、電圧のかかる順番が考え方のポイントになります。
並列回路の電流について

続いて並列回路の電流の特徴についてですが、並列回路では回路全体の電流=各箇所の電流の合計(和)となります。
電流というのは、電子の移動現象のことです。
並列回路では回路が枝分かれするため、移動する電子の数も枝分かれすることで分散し変わってしまいます。
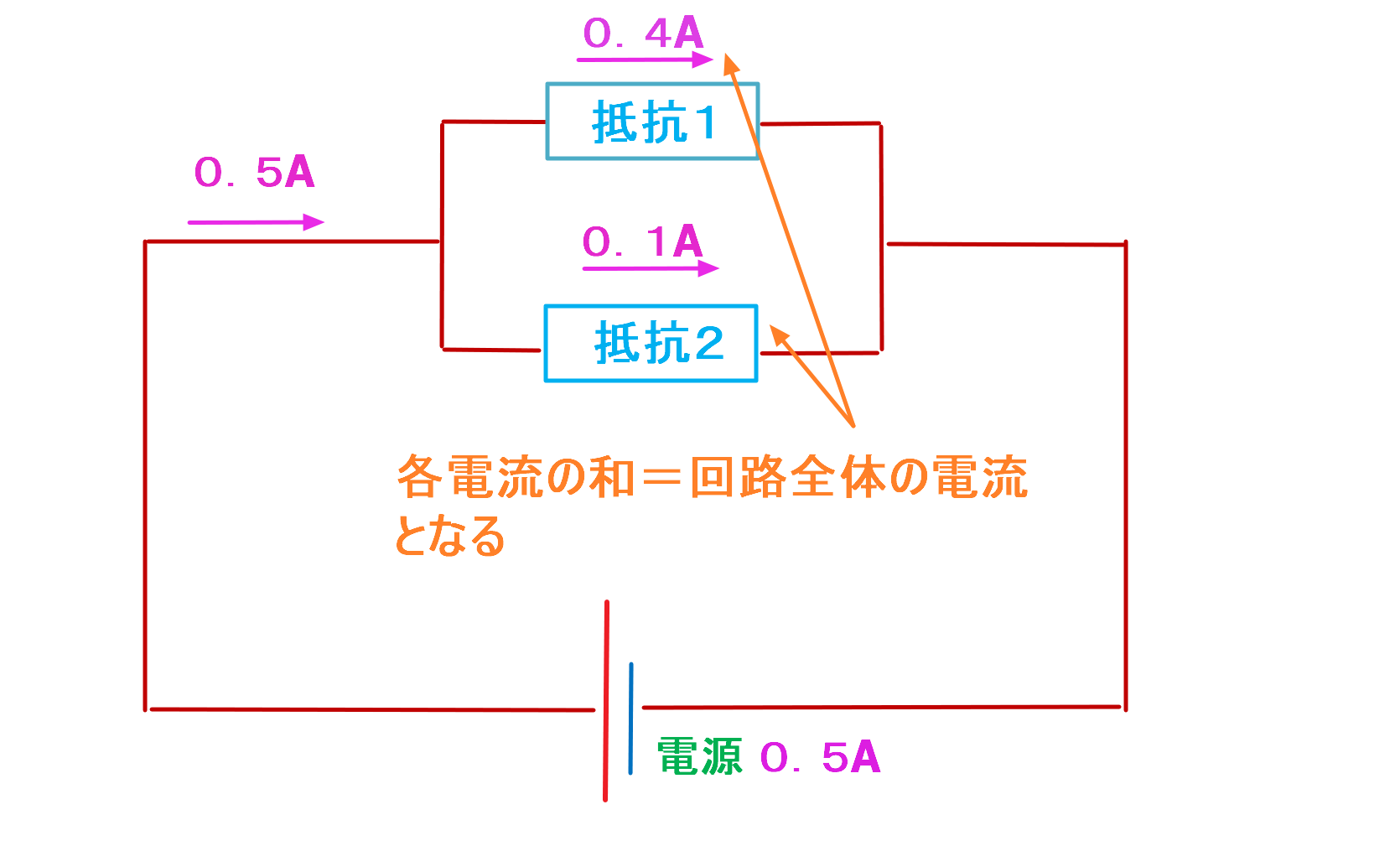
そのため、各箇所の電流の合計が回路全体の電流と等しくなります。
電流についてもオームの法則により、計算で求めることができます。
$$電流(A)=\frac{電圧(V)}{抵抗(Ω)}$$で求めることができます。
並列回路の抵抗について

並列回路の抵抗の特徴としては、回路全体の抵抗の逆数=各抵抗の逆数の合計(和)となります。
例えば下の図のような抵抗1(40Ω)、抵抗2(10Ω)の回路があり、全体の抵抗を求めるとします。

そうした場合、$$\frac{1}{回路全体の抵抗}=\frac{1}{抵抗1}+\frac{1}{抵抗2}$$で回路全体の抵抗を求めることができます。
各抵抗の逆数の合計に等しくなるという性質上、回路全体の抵抗は少なくとも抵抗1、抵抗2よりも小さな抵抗値になることが予想できます。
実際に計算をしてみると各抵抗の合計は$$\frac{1}{40}+\frac{1}{10}=0.125$$となることから、$$\frac{1}{0.125}=\frac{1}{40}+\frac{1}{10}$$となります。
よって、この回路の全体の抵抗は8(Ω)となることがわかります。
なぜこの計算式になるのかというと、並列回路全体の電流をI、抵抗1に流れる電流をI1,抵抗2に流れる電流をI2とすると、$$I=I1+I2$$となります。
上の式にオームの法則を適用すると、$$\frac{V}{回路全体の抵抗}=\frac{V}{抵抗1}+\frac{V}{抵抗2}$$となるからです。
さらに式の両辺に「回路全体の抵抗」をかけて変形すると、見覚えのある式になります。
$$V=(\frac{V}{抵抗1}+\frac{V}{抵抗2})\times{回路全体の抵抗}$$
$$回路全体の抵抗=\frac{V}{\frac{V}{抵抗1}+\frac{V}{抵抗2}}$$
$$回路全体の抵抗=\frac{1}{\frac{1}{抵抗1}+\frac{1}{抵抗2}}$$
式の各分子にあたるVについては、全て同じ数字であることから比は同じため、1とみなすことができます。
ちなみに計算式に出てくる抵抗の逆数というのは、電流の流れやすさを表すものです。
抵抗を逆数にしたものは、コンダクタンス(G)といい、単位にはジーメンス(S)が使用されます。
このコンダクタンスが大きい程、回路に電流が流れやすいということになります。
また、上の回路のような抵抗が2つある並列回路の場合は、$$回路全体の抵抗=\frac{抵抗1\times抵抗2}{抵抗1+抵抗2}$$で求めることもできます。
なぜこのような式でも計算ができるのかというと、$$回路全体の抵抗=\frac{1}{\frac{1}{抵抗1}+\frac{1}{抵抗2}}$$を変形させた式であるためです。
上記の式の右辺の分母と分子に抵抗1・抵抗2をかけて変形していくと、以下のようになります。
$$回路全体の抵抗=\frac{抵抗1\times{抵抗2}}{\frac{抵抗1\times{抵抗2}}{抵抗1}+\frac{抵抗1\times{抵抗2}}{抵抗2}}$$
分母の分数の抵抗1と抵抗2を約分すると、下記のような和分の積の形にできます。
$$回路全体の抵抗=\frac{抵抗1\times{抵抗2}}{抵抗2+抵抗1}$$
実際に計算をしてみると、$$回路全体の抵抗=\frac{40\times10}{40+10}=8(Ω)$$となり、同じ計算結果となることがわかります。
並列回路全体の抵抗の求め方は以上のことから2通りのパターンがあります。

分母と分子のどちらが和か積か間違えちゃいそう、、

もしもどっちだっけ?っとなった場合は上記の計算で導き出せれば、安心ですね!
まとめ
・並列回路とは、回路が枝分かれしている回路のことをいう
・並列回路の電圧はどこで測定をしても同じになる
・並列回路全体の電流は各箇所の電流の合計に等しくなる
・並列回路全体の抵抗の逆数と各箇所の抵抗の逆数は等しくなる
以上がまとめたものです。
今回は並列回路の計算方法と抵抗の特徴などについて解説しました。
式の意味や考え方を理解していれば、複雑な回路でも計算をすることができるようになります。
並列回路は電気回路の計算で基本となるものですが、同じく直列回路の計算についても基本となるものです。
以下の記事では、直列回路と複雑な回路の計算方法と考え方について詳しく解説をしていますので、こちらの記事もぜひ併せて読んでみてください。












並列回路の計算がわからないし、どうして分数が沢山でてくるの?