【最強のわかりやすさ】正弦波交流の実効値の計算方法を簡単に解説

交流の電気は常に大きさや向きが変化している電気です。

−になったり、０になったり、今度は＋になったりなど、とても忙しい電気です。

家のコンセントに来ている電気も交流ですが、テスターなどで電圧を測定すると、多少の変動はあるものの、一定の数値が表示されます。

交流は常に大きさが変化しているはずなのに・・・と不思議に思いませんか？

この現象には交流の実効値というものが関係しています。

今回の記事では、この交流の実効値について解説をしていきます。

この記事を読むと、実効値の計算方法と１／√２になる理由が理解できます。

実効値とは？

実効値というのは直流の電圧、または電流が、ある時間に消費した電力量と同じ電力量を消費する交流の電圧、電流のことをいいます。

直流の時と同じ電力量になる時の交流の電圧、電流ですので、電圧と電流それぞれに実効値が存在します。

下の図でいうと、直流の波形による消費電力と交流の波形による消費電力が等しい時が交流の実効値となります。

なぜこんな面倒くさい表示の仕方をする必要があるのかというと、交流の電気は常に変化しているからです。

１秒間に５０回、６０回という速さで−、０、＋を行ったり来たりします。

例えば、ブレーカーの電圧が今何Vか教えてくれ～と偉い人に頼まれた時、１秒間に５０回も数字が変わっていたら今が何Vか教えることはとても困難ですよね。

そのため、交流の電圧、電流は実効値というものを目安に取り扱いをしています。

実効値の計算方法について

それでは実効値というのは、どのように計算されて私達の普段見る数値となっているのでしょうか？

結論を最初にいいますと、実効値は瞬時値の２乗の平均値の平方根として計算されています。

頭の中が混乱してしまいそうですが、一つずつ順番に解説していきます。

まずは電力の関係について整理します。

直流の電圧をＶ、電流をＩ、抵抗をＲ、電力をPとすると電力Ｐは

$$P=V\times I[W]$$となり、オームの法則を変形させていくと

$$P=R\times I\times I=R\times I^2[W]$$となります。

交流も同じく、電圧ｖ、電流をi、抵抗をＲ、電力をpとすると最終的に

$$p=R\times i\times i=R\times i^2[W]$$という形にすることができます。

この関係を踏まえて、今度は実効値の特徴に注目します。

交流の実効値というのは先程お話したとおり、直流と交流が同じ条件下（回路や時間等）で交流の電力が直流の電力に等しくなる時が実効値とお話しました。

わかりやすいように電力が等しくなる時を図で表すと、下のようなイメージです。

交流の赤色部分、直流の青色部分の面積が同じになる時が交流の実効値になる時です。

交流の波形の面積は頑張って積分をするか、下の図のように考えることで求めることができます。

交流電力の波形を先程の直流電力の波形と重ねると下の図のようになります。

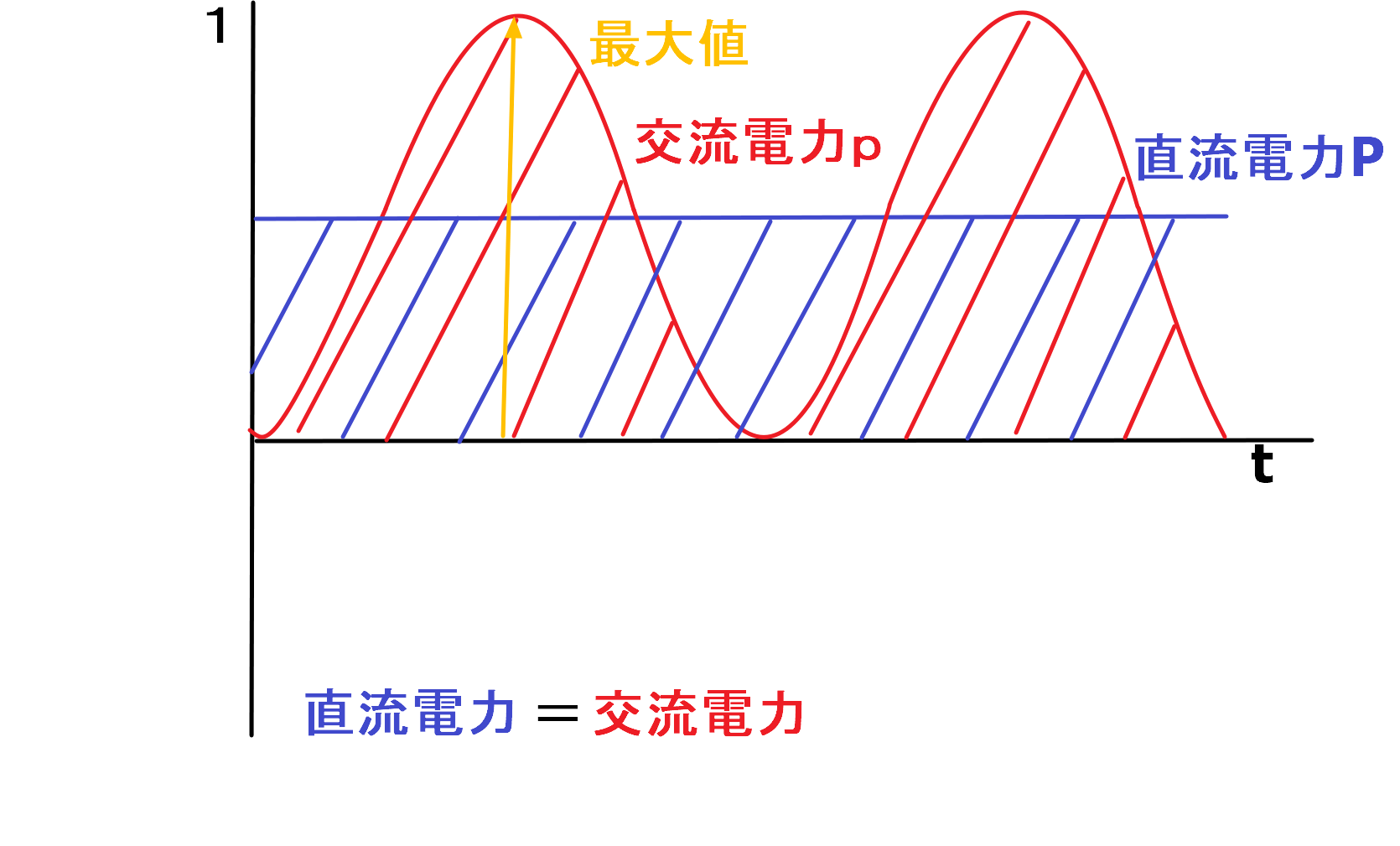
直流電力が交流電力の波形(波形の最大値）の半分の高さになることがわかります。

半分ということは、交流電力の平均値ということにもなります。

このことから、もう一度関係を整理すると

$$P=RI^2=pの平均値=Ri^2の平均値$$

$$RI^2＝Ri^2の平均値$$

$$I^2=i^2の平均値$$

Ｉの２乗を取ると、

$$I=\sqrt{i^2の平均値}・・・①$$

となります。

ちなみに２乗の平均値というのは１／２になります。

６の２乗の平均であれば１８、１００の２乗の平均であれば５０００となるように２乗の平均値は必ず１／２になります。

そのため、式①のiの２乗の平均値を1／２に置き換えると

$$I=\sqrt{\frac{1}{2}}$$

$$I=\frac{1}{\sqrt{2}}$$

となります。

また、上の式は交流電力の最大値に対する平均値なので、実効値は

$$I=\frac{1}{\sqrt{2}}\times Im$$

となります。

電流の実効値について解説しましたが、電圧の実効値も同じく交流電圧の最大値×１／√２で求めることができます。

P=VI,p=viの式をそれぞれオームの法則で電圧の２乗になるように変形させると、

$$P=V\times I[W]$$

$$P=V\times \frac{V}{R}[W]$$

$$P= \frac{V^2}{R}[W]$$

交流も同じように式を変形させ,交流電力の平均値と直流電力は等しいことから、

$$\frac{V^2}{R}=\frac{v^2}{R}の平均値・・・②$$

という関係が成り立ちます。

式②の両辺にＲをかけるとＲが消え

$$V^2=v^2の平均値$$

$$V=\sqrt{v^2の平均値}$$

となり、電流の時と同じ形になるのがわかります。

このことから、交流電圧の実効値も下の式で求められます。

$$V=\frac{1}{\sqrt{2}}\times Vm$$

長くなってしまいましたが、交流の実効値はこのような考えで計算をされ、私たちの普段見る交流の数値として表示されています。

まとめ

今回は交流の実効値について解説しました。

常に変化をしている交流でも、実効値というものがあるおかげで交流がかなり扱いやすくなります。

電気業界では実効値というのはとても重要な概念です。

また、以下の記事では実効値と関りがある正弦波交流の最大値、瞬時値について詳しく解説していますので、こちらの記事も併せて読んでみてください。

【最強のわかりやすさ】正弦波交流の平均値、瞬時値とは？簡単に解説