三相交流にはY結線、Δ結線という結線方法があります。これらの結線をすると線間電圧と相電圧というものが発生します。
「線間電圧と相電圧の違いがわからない」、「線間電圧はなぜ√3倍になるの?」と感じる方でも一つ一つ理解をしていけばわかるようになります。
今回の記事では三相交流におけるY結線とΔ結線の線間電圧、相電圧について解説をしていきます。
線間電圧と相電圧とは

三相交流回路の線間電圧と相電圧は、簡単に説明すると以下のようになります。
・線間電圧:電源と負荷をつなぐ線間に発生する電圧
・相電圧:各相に発生する電圧
線間電圧と相電圧は結線方法によって大きさや位相の関係が変化します。
三相交流回路にはY結線とΔ結線という接続方法があり、それぞれ線間電圧と相電圧の関係が異なります。
Y結線の線間電圧と相電圧
Y結線とは下記の図のように交流電源などをYの字のように接続する結線方法のことです。
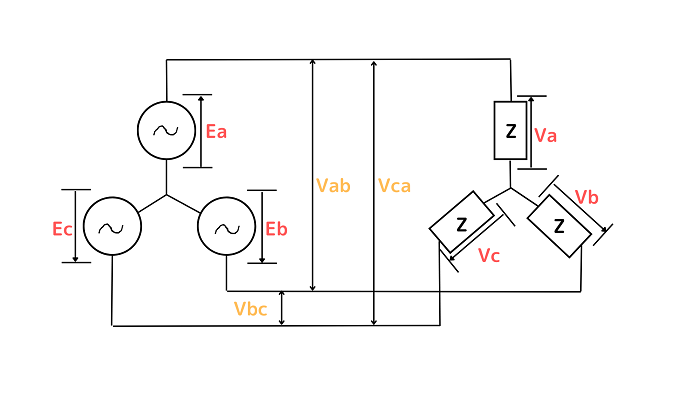
Y結線は星のような形にも見えることから星形結線や、スター結線などと呼ばれたりもします。
図でいうと、Y結線の時の線間電圧はVabやVbc、相電圧はEaやVaということになります。
Δ結線の線間電圧と相電圧
Δ結線とは下記の図のように交流電源などをΔ(三角形)のように接続する結線方法です。
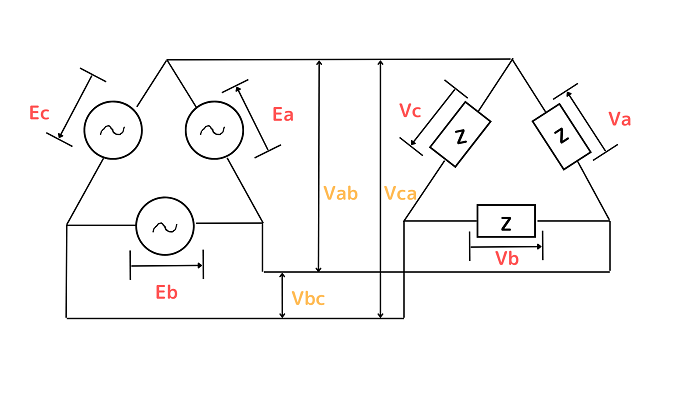
上記の図でいうとΔ結線の時の線間電圧はVabやVbc、相電圧はEaやVaということになります。
線間電圧と相電圧の違いと関係性

線間電圧と相電圧の関係性は結線方法によって違いがあります。
線間電圧と相電圧の大きさにはどのような違いがあるのか結線方法ごとに関係性を整理してみます。
Y結線の線間電圧と相電圧の関係性
下記のようなY結線で接続された三相交流回路があったとします。
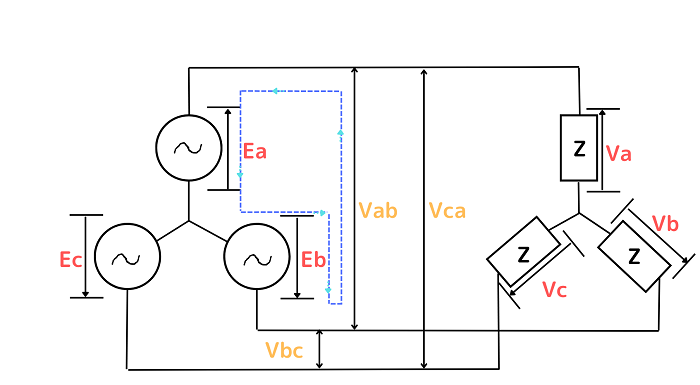
回路図の青い矢印の向きに電圧をたどっていくと、線間電圧Vabの間に直列(一直線)に相電圧EaとEbがあります。
一巡する閉回路において、各箇所に発生する電圧や起電力(電源電圧)の合計は0になります。(キルヒホッフの第1法則)
キルヒホッフの第1法則については下記の記事で解説してますので気になる方は参考にしてください。【最強のわかりやすさ】キルヒホッフの第2法則について簡単に解説
矢印の向きを基準として線間電圧と相電圧を合計していくと以下の関係が成り立ちます。
$$Vab+(-Ea)+Eb=0$$
$$Vab=Ea-Eb・・・①$$
式による関係性を整理できたので、今度はベクトルで大きさと位相の違いを見ていきます。
Y結線の線間電圧は相電圧の√3倍になる
Y結線の三相交流回路では線間電圧が相電圧の√3倍になります。
線間電圧が√3倍になる理由はベクトル図を見るとよくわかります。
例えば、下記のような交流回路があったとします。

上記の三相交流回路の相電圧をベクトルにすると下記のようなベクトルになります。
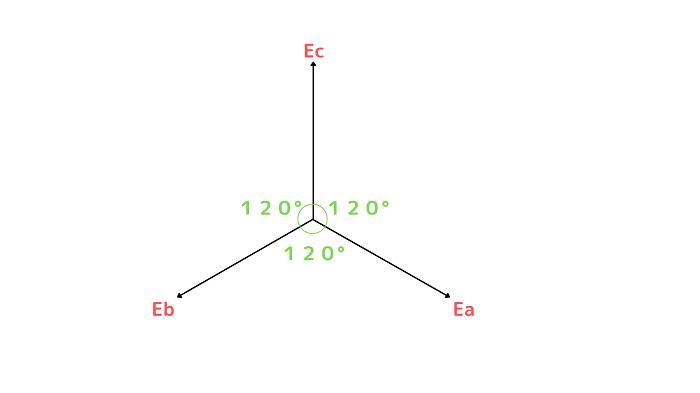
各相の相電圧は120°の位相差があり、大きさは全て同じ大きさです。
このベクトルに線間電圧のベクトルを描くと、線間電圧Vabのベクトルは下記のようになります。

なぜ線間電圧がこのようなベクトルになるのかというと、先程の①の関係式(Vab=Ea-Eb)から導き出したからです。
線間電圧VabはVab=Ea+(-Eb)と同じため、相電圧EaとEbの180°反対のベクトル(-Eb)を合成したものになります。
また、線間電圧のベクトルに90°の補助線を引いてさらに注目すると下記のようになります。
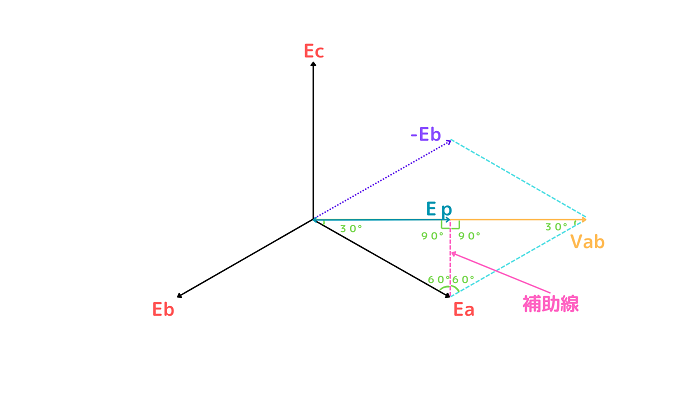
補助線とと相電圧の角度の関係から以下の式が導きだせます。
$$\cos{30°}=\frac{Ep}{Ea}$$
$$Ep=Ea×\cos{30°}=Ea×\frac{\sqrt{3}}{2}$$
二等辺三角形の性質からEpは線間電圧Vabの半分であるため、線間電圧は下記の式になります。
$$Vl(Vab)=Ep×2=Ea×\cos{30°}×2$$
$$=Ea×\frac{\sqrt{3}}{2}×2=Ea×\sqrt{3}$$
このことから、線間電圧の大きさは相電圧の√3倍になることがわかります。
Y結線の線間電圧は相電圧よりも位相が30°進む
Y結線の三相交流回路では線間電圧の位相が相電圧よりも30°進みます。
位相が30°進む理由はこれも各電圧をベクトルにしてみるとよくわかります。
先程と同じように相電圧と線間電圧をベクトルにすると下記のようなベクトルになります。
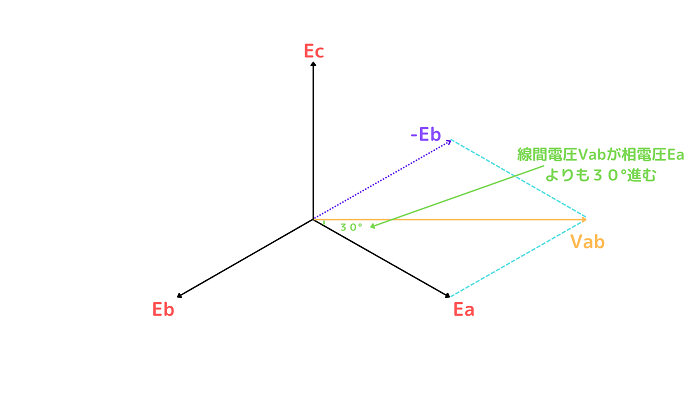
合成して描いた線間電圧のベクトルが相電圧よりも30°反時計回り方向に位置していることがわかります。
Δ結線の線間電圧と相電圧は同じになる
Δ結線の場合、線間電圧と相電圧は大きさも位相も同じになります。
例えば下記のようなΔ結線で接続された三相交流回路があったとします。
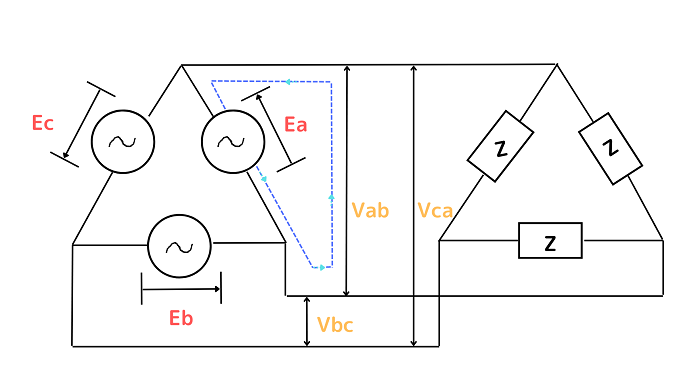
回路図の青い矢印の向きに一巡する閉回路の電圧をたどっていくと、線間電圧Vabと相電圧Eaがあります。
しかし、相電圧Eaは線間電圧Vabと共通の部分(同じ部位)の電圧と言えるため、全く同じ電圧となります。
Y結線の時のみ線間電圧が√3倍になり、位相が30°進みます(相電圧よりも)
線間電流と相電流とは

電流にも電圧と同じく、線電流と相電流があります。
三相交流回路の線電流と相電流は、簡単に説明すると以下のようになります。
・線電流:電源と負荷をつなぐ線に流れる電流
・相電流:各相に流れる電流
線電流と相電流もY結線か、Δ結線かによって大きさや位相の関係が変化します。
Y結線の線電流と相電流
Y結線の線電流と相電流は下記の図のとおりです。

図でいうと、Y結線の時の線電流はIabやlbc、相電流はIaやlbということになります。
Δ結線の線電流と相電流
Δ結線の線電流と相電流は下記の図のとおりです。

図でいうと、Δ結線の時の線電流はIabやlbc、相電流はIaやlbとなります。
線電流と相電流の違いと関係性

線電流と相電流についても結線方法によって大きさや位相の関係性に違いがあります。
結線方法ごとの関係性は主に下記のとおりです。
Y結線の線電流と相電流は同じになる
Y結線の線電流と相電流はなぜ同じになるのかというと、1相分の電流が線電流でもあるためです。
例えば下記のようなY結線で接続された三相交流回路があったとします。
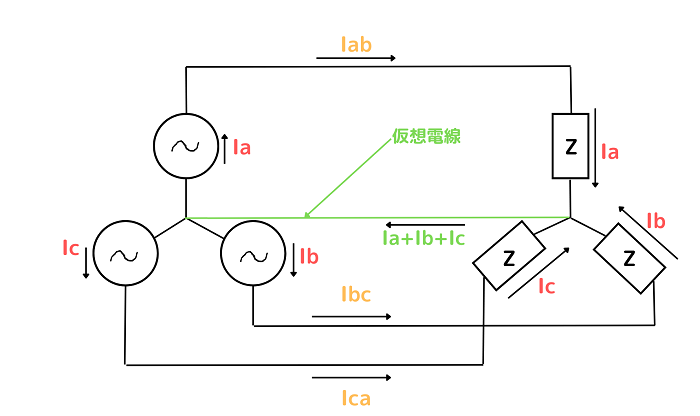
電源と負荷の各相の中心(中性点)に1本の電線が接続されていることを仮想すると、戻りの電流が仮想電線を流れます。
仮想電線には3相分の戻りの電流が流れることになり,各相に閉回路ができることから相電流と線電流は同じものになります。
しかし、各相の電源と負荷の大きさが同じである対象三相交流の場合、この仮想電線に電流は流れません。
対象三相交流の電流は三相分の電流のベクトルを合計すると互いに打ち消し合い、全体としては0になるためです。
三相分の電流ベクトルの合計が0になる理由は以下の記事を参考にしてください。【最強のわかりやすさ】三相交流のベクトル図について簡単に解説
そのため仮想電線がある場合と無い場合でも回路の状態は同じと言えます。
このことから普通のY結線の時でも線電流と相電流は同じになることがわかります。
Δ結線の線電流と相電流の関係性
下記のようなΔ結線で接続された三相交流回路があったとします。

線電流Iabの向きを基準とすると、線電流Iabは相電流IaとーIc(反対向きの相電流)の合計となります。
他の箇所も同じように考えると以下の式が成り立ちます。
$$Iab=Ia+(-Ic)・・・②$$
$$Ibc=Ib+(-Ia)$$
$$Ica=Ic+(-Ib)$$
この関係性を踏まえてベクトル図にすると大きさや位相の違いがわかってきます。
Δ結線の線電流は相電流の√3倍になる
Δ結線の三相交流回路では線電流が相電流の√3倍になります。
線電流が√3倍になる理由はY結線の線間電圧が√3倍になる時と似ており、ベクトル図をよく見るとわかります。
例えば下記のような交流回路があったとします。

上記の三相交流回路の相電流をベクトルにすると下記のようなベクトルになります。
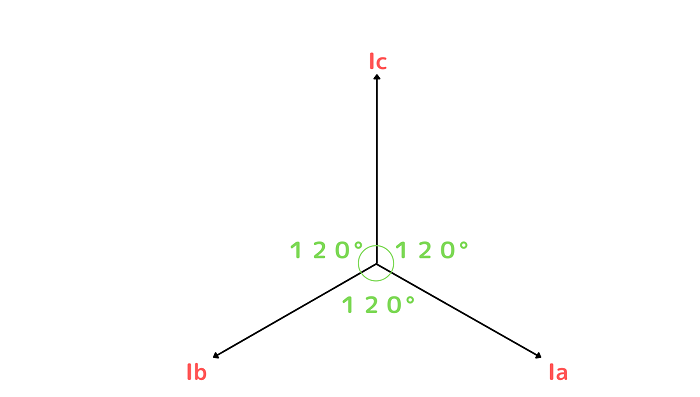
このベクトルに線電流のベクトルを描くと、線電流Iabのベクトルは下記のようになります。
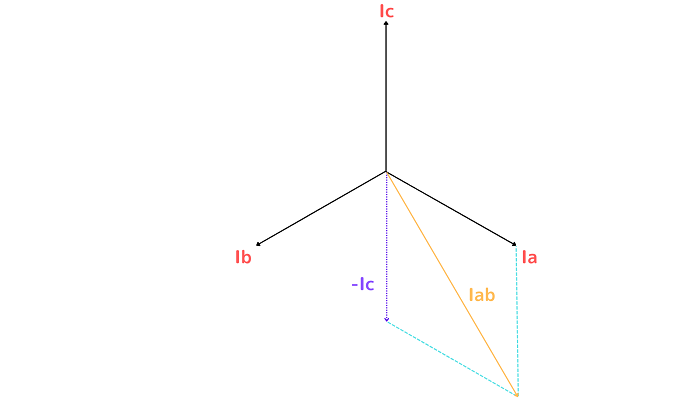
なぜ線電流がこのようなベクトルになるのかというと、先程の②の関係式から導き出したからです。
線電流IabはIab=Ia+(-Ic)のため、相電流IaとIcの180°反対のベクトル(-Ic)を合成したものになります。
また、線電流のベクトルに90°の補助線を引いてさらに注目すると下記のようになります。

補助線と相電流の角度の関係から以下の式が導きだせます。
$$\cos{30°}=\frac{Ip}{Ia}$$
$$Ip=Ia×\cos{30°}=Ia×\frac{\sqrt{3}}{2}$$
二等辺三角形の性質からIpは線電流Iabの半分であるため、線電流は下記の式になります。
$$Il(Iab)=Ip×2=Ia×\cos{30°}×2$$
$$=Ia×\frac{\sqrt{3}}{2}×2=Ia×\sqrt{3}$$
このことから、線電流の大きさは相電流の√3倍になることがわかります。
Δ結線の線電流は相電流よりも位相が30°遅れる
Δ結線の三相交流回路では線電流の位相が相電流よりも30°遅れます。
位相が30°遅れる理由はこれも各電圧をベクトルにしてみるとよくわかります。
先程と同じように相電流と線電流をベクトルにすると下記のようなベクトルになります。

合成して描いた線電流のベクトルが相電流よりも30°時計回り方向に位置していることがわかります。
Δ結線の時のみ線電流が√3倍になり、位相が30°遅れます(相電圧よりも)
まとめ
・線間電圧:電源と負荷をつなぐ線間に発生する電圧
・相電圧:各相に発生する電圧と電流
・線電流:電源と負荷をつなぐ線に流れる電流
・相電流:各相に流れる電流
・Y結線では線間電圧が相電圧よりも√3倍大きくなり、位相が30°進む
・Δ結線では線電流が相電流よりも√3倍大きくなり、位相が30°遅れる
以上、今回は線間電圧と線電流、相電圧と相電流についての解説でした。
線間電圧と相電圧については三相交流回路において基本となる重要な知識です。
また、三相交流回路のさらに基本となるのが単相交流回路の計算です。
以下の記事では単相交流回路の位相や計算方法について解説していますので併せてぜひ読んでみてください。
【最強のわかりやすさ】位相の遅れと進みとは?電気の位相を解説!








この記事を読むと、線間電圧と相電圧、線電流と相電流の違いについてわかるようになります!