電気を妨げるものには抵抗、コイル、コンデンサなどがあり、これらは総称してインピーダンスと呼ばれています。
インピーダンスの計算は交流回路の計算の基本であり、直列か並列かによっても変わってきます。
しかし「インピーダンスの計算は複雑で難しい」、「なぜこの式で計算ができるんだろう?」と感じませんか?
今回は並列回路のインピーダンスの計算方法について解説します!
RL並列回路のインピーダンスについて

まずはR(抵抗)とL(コイル)を並列に接続した場合のインピーダンスの計算についてです。
RとLの並列回路のインピーダンスは下記の式で計算することができます。
$$Z=\frac{V}{I}=\frac{1}{\sqrt{\frac{1}{R^2}+\frac{1}{XL^2}}}$$
$$=\frac{RXL}{\sqrt{R^2+XL^2}}[Ω]$$
なぜこのような式になるのかというと、電流と電圧の位相関係を踏まえてオームの法則にあてはめるとこのような式になるためです。(XLのLは表示の関係上大きい文字にしています)
例えば下の図のような抵抗とコイルを並列に接続した回路の全体のインピーダンスを考えてみます。
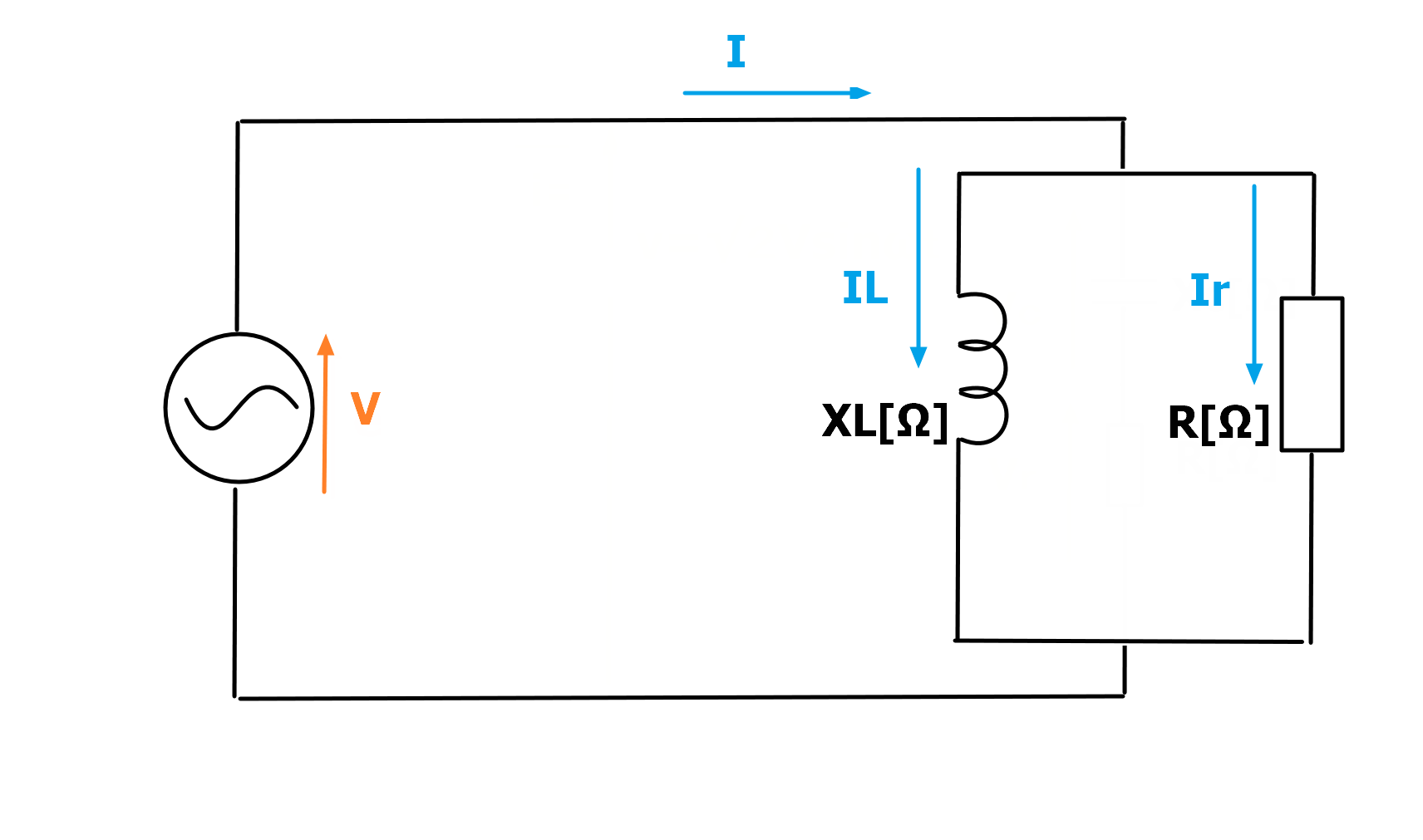
回路全体のインピーダンスを求めるとなると、オームの法則により、回路全体の電流と電圧を最初に求めなければ計算することができません。
電圧Vは並列回路なのでどこでも同じ電圧となります。
次に全体の電流Iについて考えてみます。
並列回路全体の電流は各箇所の電流の合計になるため、IrとILの合計になります。
しかし、交流回路にコイルが接続されている場合、電圧Vと電流ILには90°の位相差が発生します。(電流の位相が90°遅れる)
これはコイルの自己誘導作用によってコイルの電流が妨げられ、電流の位相が90°遅れてしまうためです。
位相の関係を踏まえて、電流I、Ir、ILと電圧Vをベクトル図で表すと下の図のようになります。
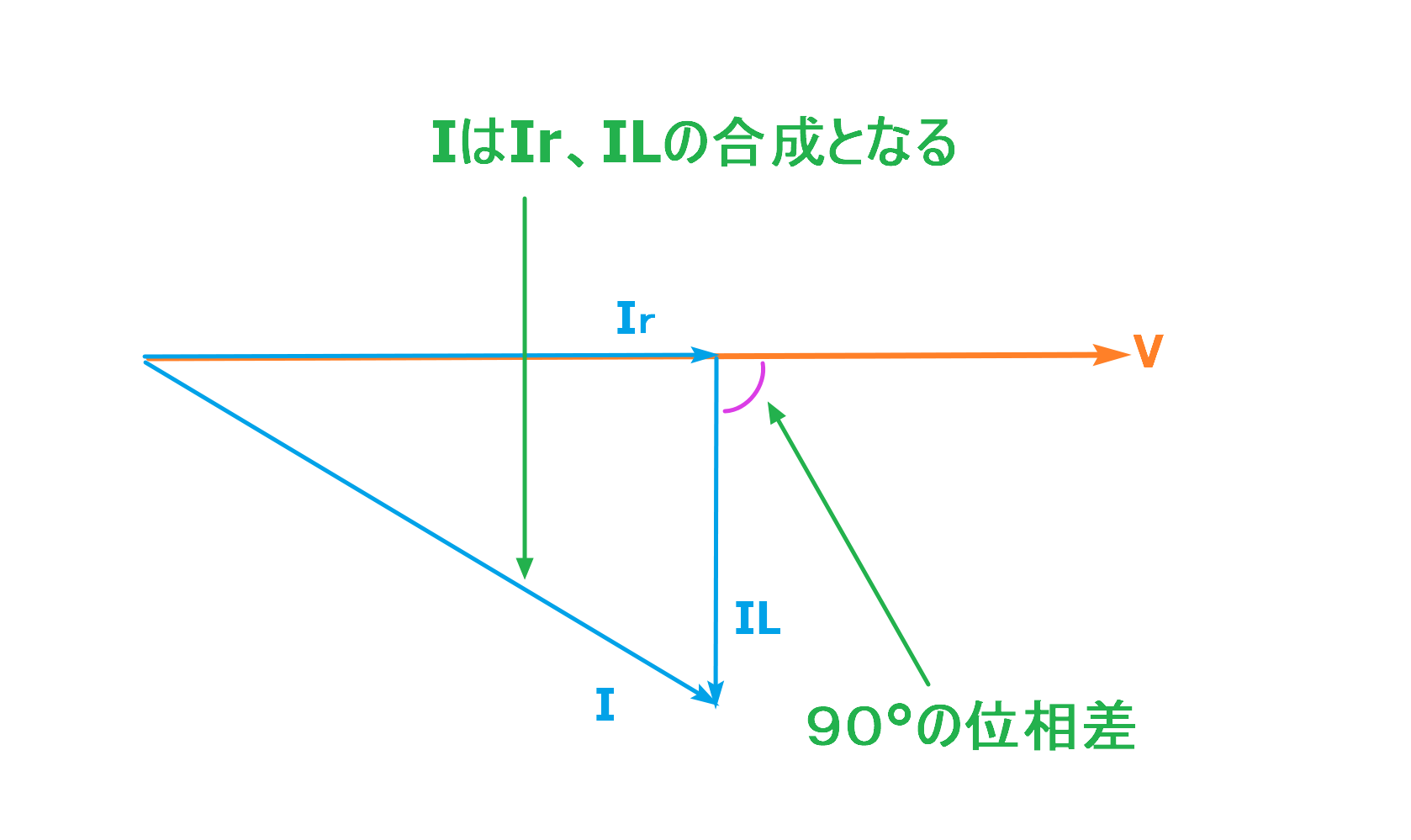
先程電流IはIrとILの合計になるとお話しましたが、残念ながら直流回路のように足し算をするだけでは求めることはできません。
上のベクトル図で電流Iは電流IrとILの合計になることから、2つのベクトルを合成したものが電流Iとなります。
そうすると、電流I、Ir、ILで直角三角形が形成されるため三角関数の性質から電流Iは下記の式で求められることになります。
$$I=\sqrt{Ir^2+IL^2}=\sqrt{(\frac{V}{R})^2+(\frac{V}{XL})^2}$$
$$=V\sqrt{\frac{1}{R^2}+\frac{1}{XL^2}} [A]・・・①$$
①の式をZ=V/Iにあてはめると、最初に説明したインピーダンスの計算式になることがわかります。
これがRとLを並列に接続した時の回路全体のインピーダンスを求められる根拠です。
交流回路の計算では最初に電流や電圧をベクトルに描き、位相関係を整理してから計算をするとわかりやすいです。
RC並列回路のインピーダンスについて

今度はR(抵抗)とC(コンデンサ)を並列に接続した場合のインピーダンスの計算についてです。
RとCの並列回路のインピーダンスは下記の式で計算することができます。
$$Z=\frac{V}{I}=\frac{1}{\sqrt{\frac{1}{R^2}+\frac{1}{Xc^2}}}$$
$$=\frac{RXc}{\sqrt{R^2+Xc^2}}[Ω]$$
なぜこのような式になるのかというと、これも電流と電圧の位相関係をもとにオームの法則で導きだしているためです。
例えば下の図のような抵抗とコンデンサを並列に接続した回路の全体のインピーダンスを考えてみます。
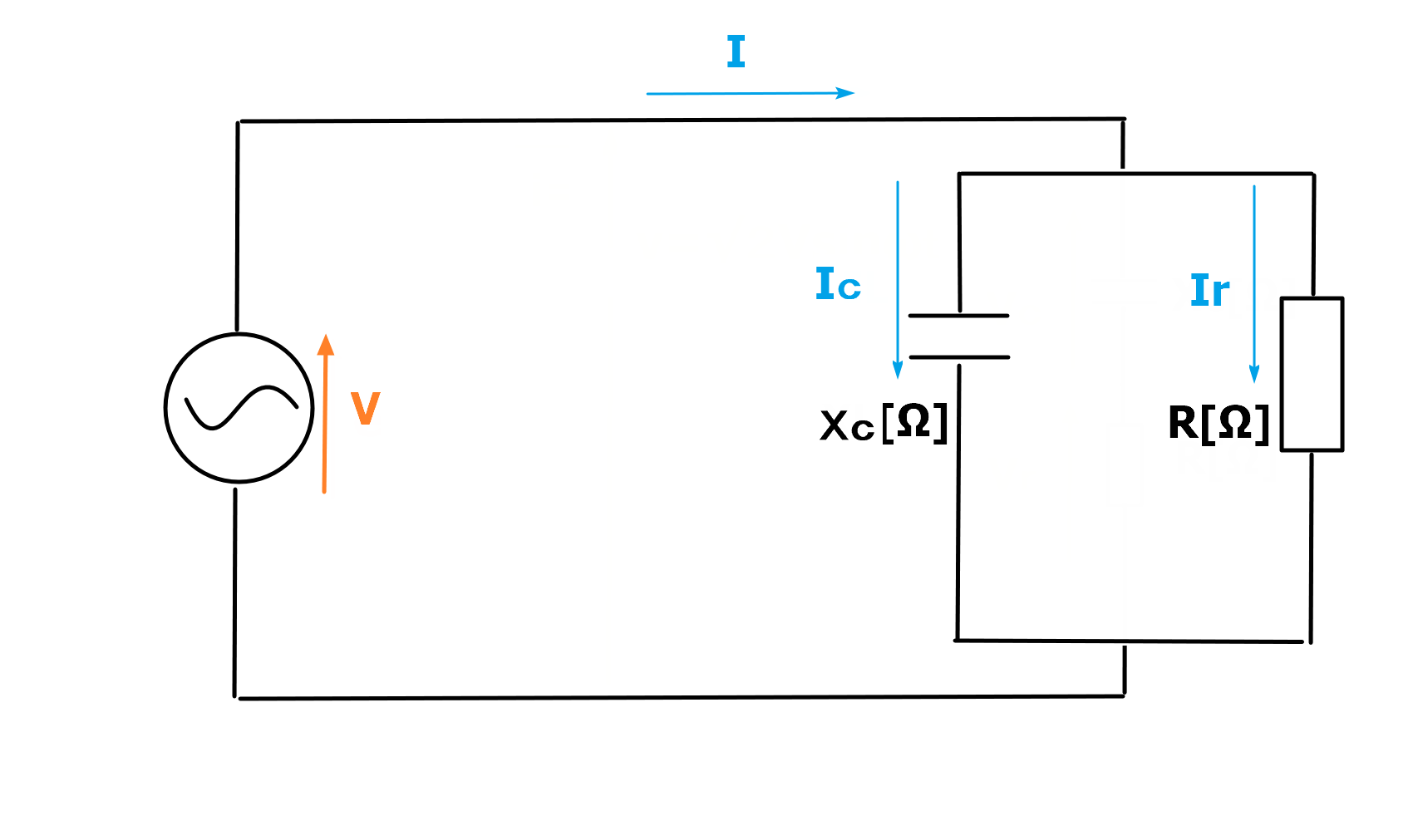
RとLの時と同じように、回路全体のインピーダンスを求める時は、回路全体の電流と電圧を最初に求めなければ計算することができません。
全体の電圧Vと電流Iの考え方も先程と同じです。
並列回路のため電圧Vはどこでも同じになり、電流Iは電流IrとIcの合計になります。
しかし電流Icの位相については電圧Vよりも90°進んだ位相となります。
これはコンデンサに電荷を蓄える性質があるため、電源との電位差がなくなり、大きさの変化にズレが発生することから位相差が生まれるものです。
これらのことを踏まえて電圧Vと電流I、Ir、Icの関係をベクトル図に表すと下の図のようになります。
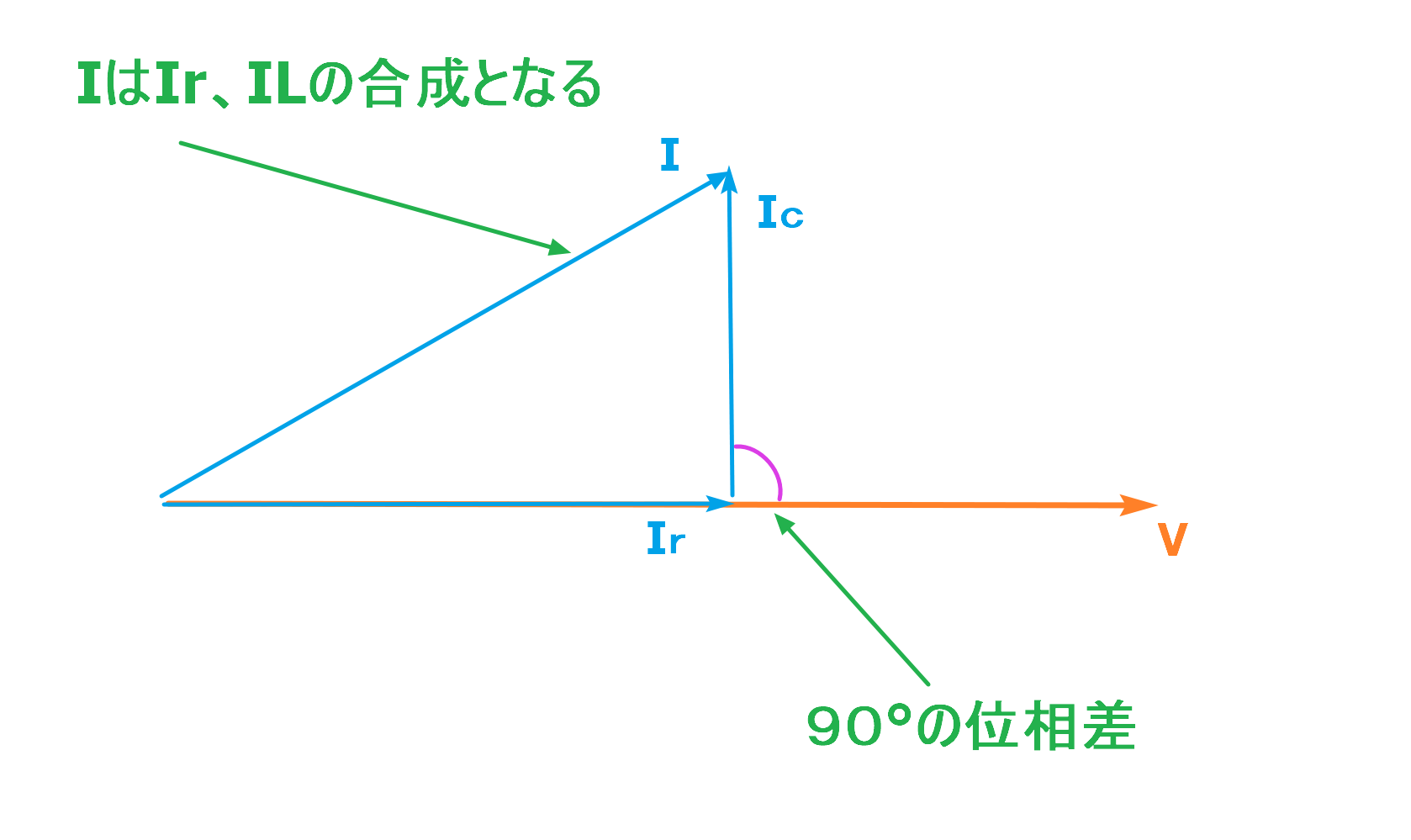
並列回路の電流Iは各電流IrとIcの合計になることから、2つのベクトルを合成したものが電流Iとなります。
そうするとRとLの時とは反対方向にまた直角三角形が形成されるため、三角関数の性質から電流Iは下記の式で求められます。
$$I=\sqrt{Ir^2+IL^2}=\sqrt{(\frac{V}{R})^2+(\frac{V}{XL})^2}$$
$$=V\sqrt{\frac{1}{R^2}+\frac{1}{XL^2}} [A]・・・②$$
②の式をZ=V/Iにあてはめると、はじめに説明したインピーダンスの計算式になることがわかります。
これがRとCを並列に接続した時の回路全体のインピーダンスを求められる根拠です。
RとLの時と求め方は同じですが、コンデンサの電流は位相関係が違うため注意しましょう。
RLC並列回路のインピーダンスについて

最後はR(抵抗)、L(コイル)、C(コンデンサ)を並列に接続した場合のインピーダンスの計算についてです。
R、L、Cの並列回路のインピーダンスは下記の式で計算することができます。
$$Z=\frac{V}{I}=\frac{1}{\sqrt{\frac{1}{R^2}+(\frac{1}{XL}-\frac{1}{Xc})^2}} [Ω]$$
なぜこのような式になるのかというと、これも電流と電圧の位相関係をもとにオームの法則で導きだしているためです。
先程までの考え方と基本は同じです。
全体の電圧と電流の大きさと位相関係に注意してオームの法則に当てはめて計算するだけです。
今度は下の図のような抵抗、コイル、コンデンサを並列に接続した回路で考えてみます。
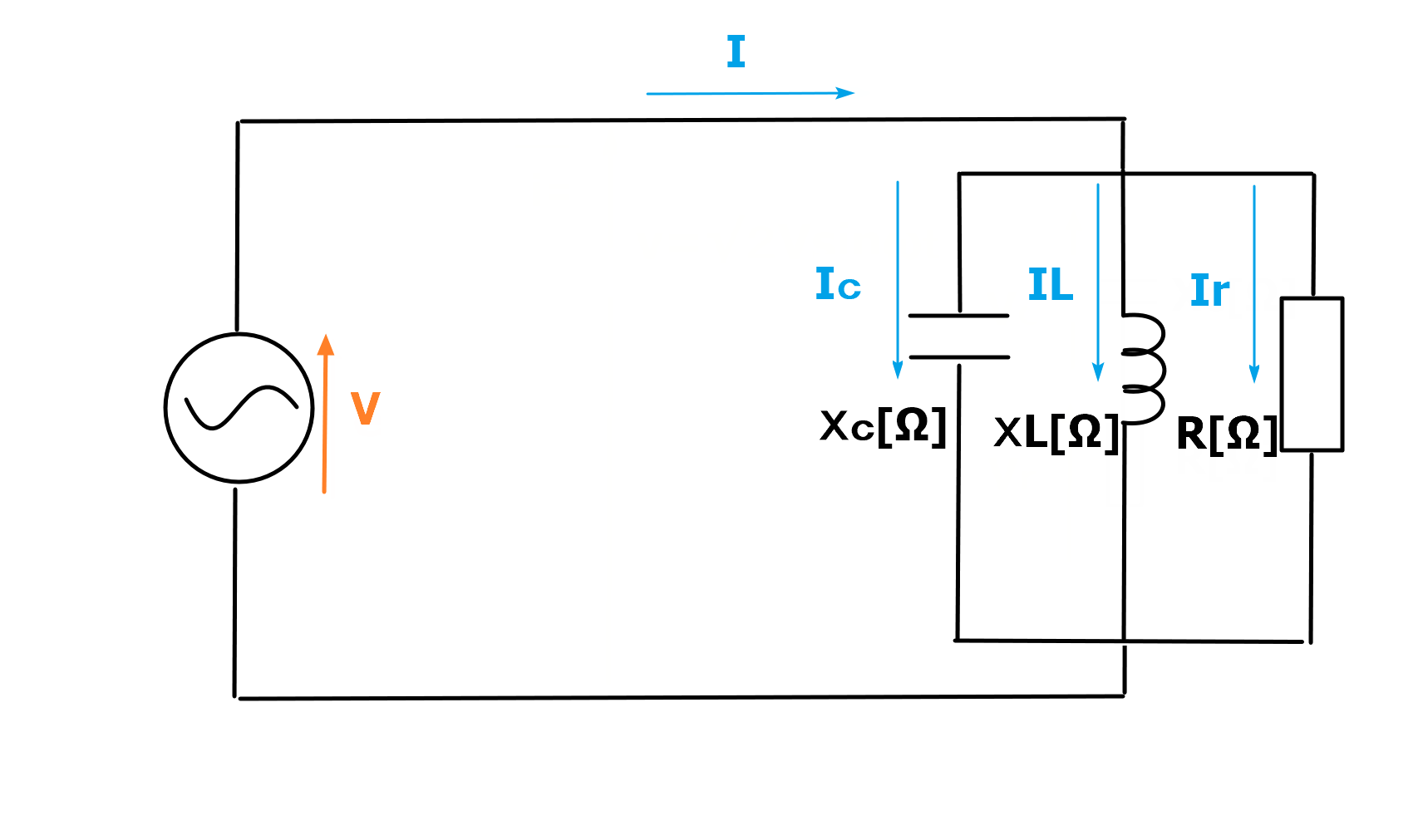
電圧Vはどこでも同じになり、全体の電流Iは各箇所の電流(Ir、IL、Ic)の合計になります。
位相関係については先程解説したとおり、電圧Vに対して電流ILが90°遅れ、電流Icが90°進んだ関係になります。
ことことを踏まえて電圧Vと電流I、IL、Icをベクトル図で表すと下の図のようになります。
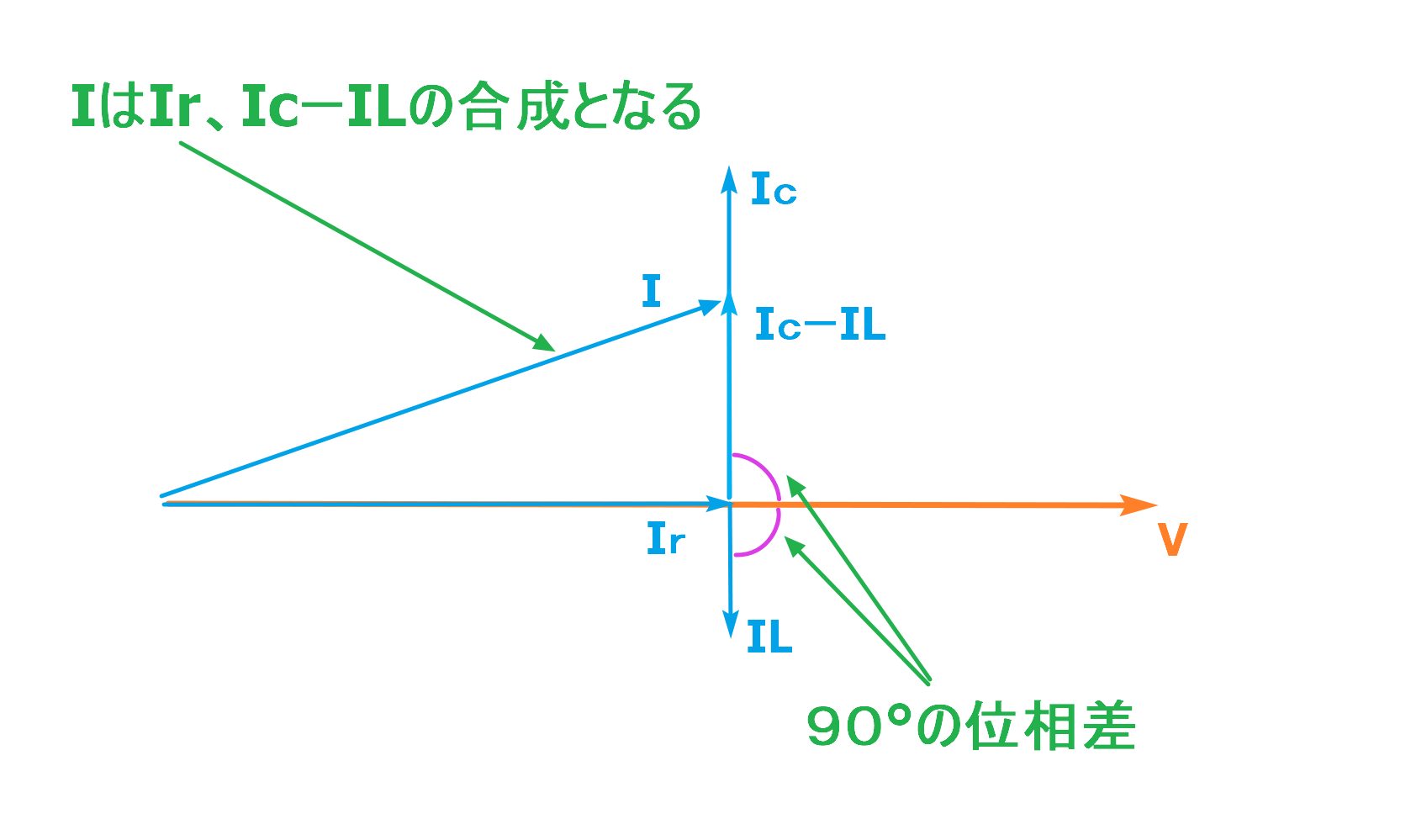
上の図で注目しなければいけないのは、ILとIcのベクトルです。
ILとIcについては電圧Vに対して90°ずつ位相がズレていることから、180°反対の向きになり互いに打ち消し合います。
並列回路の電圧Vはどこでも一定であることから、オームの法則によりIL、Icの大きさはXLとXcの大きさにより変化します。(今回はXc>XL)
また、電流Iは各電流の合計になることから、全ての電流のベクトルを合成したものです。
よって、XL>Xcの時は電流Iは遅れの位相、Xc>XLの時は進みの位相ベクトルになります。(上記ベクトルは進み)
IL、Icのどちらが大きくても、直角三角形が形成されるため三角関数の性質から電流Iは下記の式で求められます。
$$I=\sqrt{Ir^2+(IL-Ic)^2} [A]$$
$$=V\sqrt{\frac{1}{R^2}+(\frac{1}{XL}-\frac{1}{Xc})^2} ・・・③ [A]$$
③の式をZ=V/Iに当てはめると、はじめに説明したインピーダンスの計算式になることがわかります。
以上がR、L、Cを並列に接続した時の回路全体のインピーダンスを求める方法です。
IL、Icの大きさに注意をしながら計算をしましょう。
まとめ
・RとLの並列回路のインピーダンス
$$Z=\frac{RXL}{\sqrt{R^2+XL^2}}[Ω]$$
・RとCの並列回路のインピーダンス
$$Z=\frac{RXc}{\sqrt{R^2+Xc^2}}[Ω]$$
・R、L、Cの並列回路のインピーダンス
$$Z=\frac{1}{\sqrt{\frac{1}{R^2}+(\frac{1}{XL}-\frac{1}{Xc})^2}} [Ω]$$
以上、今回はインピーダンスの並列回路についての解説でした。
交流回路の計算をする時は、インピーダンスを求めることが必須になりますのでとても重要です。
また、インピーダンス王になるためにはコイルとコンデンサの性質を理解することも重要になってきます。
下記の記事ではコイルとコンデンサの性質について詳しく解説していますので、あわせて是非参考にしてください。










コメントを残す