「コンデンサって聞いたことはあるけど何だろう?」そう感じたことはありませんか?
現代は電子機器であふれており、とても便利な生活をすることができます。
その電子機器を支えているものの一つにコンデンサというものがあります。
今回はそんなコンデンサの概要、計算方法などを詳しくお話していきます。
コンデンサとは?

そもそもコンデンサとは一体何なのかというと、電荷を蓄えられるようにした物のことをいいます。
電荷というのは、原子の周りにある電子が移動することによって、電気を帯びた物体がもつ電気の量のことをいいます。
コンデンサの構造は2つの導体とその間に絶縁物をはさむような構造をしています。
この2つの導体に電荷が蓄えられるようなイメージです。

例えば下の図のようなコンデンサがあったとします。

電圧を加えることにより電流が流れ、2つの導体にーと+の電荷が送られます。
電源をOFFにしても導体には電荷が残り、導体間に電圧も残るという仕組みになっています。
しかし、蓄えられた電荷は無限に残る訳ではなく、いつかは完全に放電します。
時間と共に回路内へ移動するため、電圧も徐々に下がりいつかは0になります。
どうしてもコンデンサの電荷を放電したい時は抵抗を繋ぐことで放電できますが、抵抗値の低いもので放電をすると大電流が流れ、焼損する恐れもあり危険です。
放電する時には必ず高抵抗の抵抗を使用し、ゆっくり放電をすることが大切です。
このようにコンデンサは電荷を蓄えたり、放電したりする性質を持つことから、電子機器の出力をあげるなど様々な場面で使用されています。
コンデンサが蓄える電荷の量について

コンデンサの蓄えることができる電荷の量は静電容量と呼びます。
単位にはF(ファラド)、量記号にCを使われています。
コンデンサの蓄えられる電荷の量は静電容量、回路の電圧により変化するため、意図的に蓄えられる量を調整することができます。
コンデンサの静電容量を大きくするには、導体の面積を大きくする、導体間の距離を短くする、絶縁体に使用する物質を変えるなどの方法があります。
また、回路の電圧が高い程、コンデンサに蓄えられる電荷の量は多くなります。
これらのことからコンデンサの静電容量は下記の式で計算して求めることもできます。
$$C=Q/V[F]$$
ちなみに、静電容量が1Fのコンデンサは、電圧が1V加わった時に1Cの電荷を蓄えられるコンデンサということになります。
コンデンサの並列接続

コンデンサを複数使用した場合、回路全体の静電容量は接続の仕方によって計算方法が変わってきます。
まず、コンデンサの並列回路では、回路全体の静電容量は各コンデンサの静電容量の合計(和)となります。
例えば下の図のような回路の電圧がV3、コンデンサC1、C2に蓄えられる電荷をそれぞれQ1、Q2としてコンデンサを並列に接続した回路があったとします。

コンデンサの静電容量は上の記事でC=Q/V[F]とお話しました。
そして並列回路の電圧はどこでも同じ電圧になります。
そのため、Q1=C1V3、Q2=C2V3という式が成り立ちます。
回路全体の蓄えられた電荷をQ3とすると、Q3=Q1+Q2となるため、Q3=(C1+C2)V3となります。
C3=Q3/V3であることから、上の式を代入すると、C3=(C1+C2)V3/V3となり、
$$C3=C1+C2$$
となります。
このことから、コンデンサを並列に接続した時の回路全体の静電容量は各コンデンサの静電容量の合計(和)となることがわかります。
コンデンサの直列接続

今度はコンデンサを直列に接続すると静電容量はどうなるのでしょうか?
コンデンサを直列に接続した時、回路全体の静電容量は各コンデンサの静電容量の逆数の合計(和)を逆数にしたものとなります。
言葉のみですと凄くわかりにくく、混乱しそうですので順番に説明していきます。
例えば下の図のような電源の電圧をV3、コンデンサC1、C2に蓄えられる電荷をそれぞれQ1、Q2としてコンデンサを直列に接続した回路があったとします。
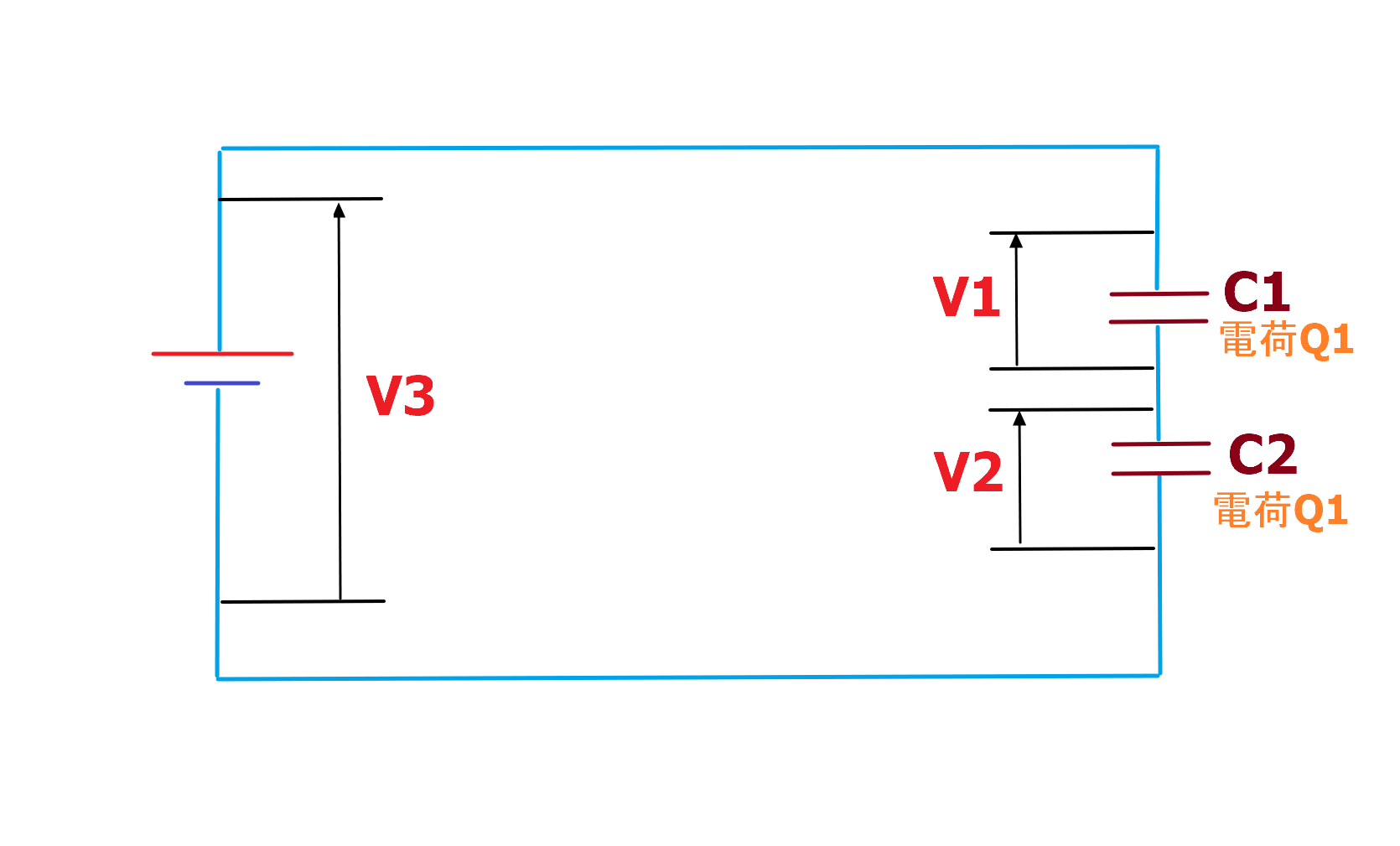
直列回路では電流の通り道が1本であることから、回路に流れる電荷の量はどこでも等しくなり、Q1=Q2となります。
このことから、回路全体の蓄えられる電荷Q3はQ3=Q1=Q2となります。
また、C=Q/Vの関係から、Q3=C1V1=C2V2となり、各コンデンサにかかる電圧はV1=Q3/C1、V2=Q3/C2という関係が成り立ちます。
直列回路では各電圧の合計が回路全体の電圧となることから、回路全体の電圧はV3=V1+V2=Q3(1/C1+1/C2)となります。
回路全体の静電容量はC3=Q3/V3であることから、V3に上の式を代入すると、
$$C3=\frac{1}{\frac{1}{C1}+\frac{1}{C2}}$$
となります。
このことから、回路全体の静電容量は各静電容量の逆数の合計をさらに逆数にすることで求められることがわかります。
まとめ
・コンデンサは電荷を蓄えたり、放電する性質がある
・コンデンサは2つの導体の間に絶縁物を入れることで電荷を蓄えている
・コンデンサの並列回路では回路全体の静電容量は各コンデンサの静電容量の合計(和)となる
・コンデンサの直列回路では回路全体の静電容量は各コンデンサの静電容量の逆数を合計し、さらに逆数にしたものになる
以上がまとめたものです。
今回は一度くらいは聞いたことがありそうなコンデンサについての説明でした。
エネルギーを蓄えるという便利な性質があるため、様々な機器に使用されていることを理解していただけたかと思います。
今回の記事で少し出てきました直列回路、並列回路の考え方も電気回路の基本となる大切な内容ですので、下の記事も併せて是非読んでみてください。








コメントを残す