【最強のわかりやすさ】正弦波交流の平均値、瞬時値とは？簡単に解説

電気には直流、交流の２種類の電気があります。

その中でも交流は正弦波交流とも呼ばれており、大きさ、向きが周期的に変化する電気です。

常に変化をしている電気の大きさを表すのは難しいですよね。

そのため、正弦波交流の大きさを表したい時は、場面に応じて様々な表し方をします。

今回は正弦波交流の大きさの表し方について解説していきます。

この記事を読むと、正弦波交流の平均値と瞬時値について理解することができます。

正弦波交流の最大値とは

まず、正弦波交流というのは下の図のように周期的に電気の向き、大きさが変わることで、正弦波となる電気のことをいいます。

最大値というのはこの波形の中で、山になっている部分（矢印の部分）のことをいいます。

文字通り波形の中で一番大きくなる部分が最大値となります。

最大値は電圧であればEｍやＶｍ、電流であればＩｍとよく表現されます。

周期的に変化する大きさの中で一番大きい時の電圧、電流を表現したい！という時に使用されるのが最大値です。

正弦波交流の瞬時値とは

正弦波交流には瞬時値という表現もあります。

交流の電気は常に大きさ、向きが変化しているため、あるタイミング（位相）の時の大きさを表したい時に使用されます。

決まったタイミングの時の大きさを表せるため、交流の表し方としてよく使われる表し方です。

どのように瞬時値を表すのか、下の図の正弦波形を左のベクトルにプロットした図を使ってe1、e2の波形を瞬時値で表してみます。

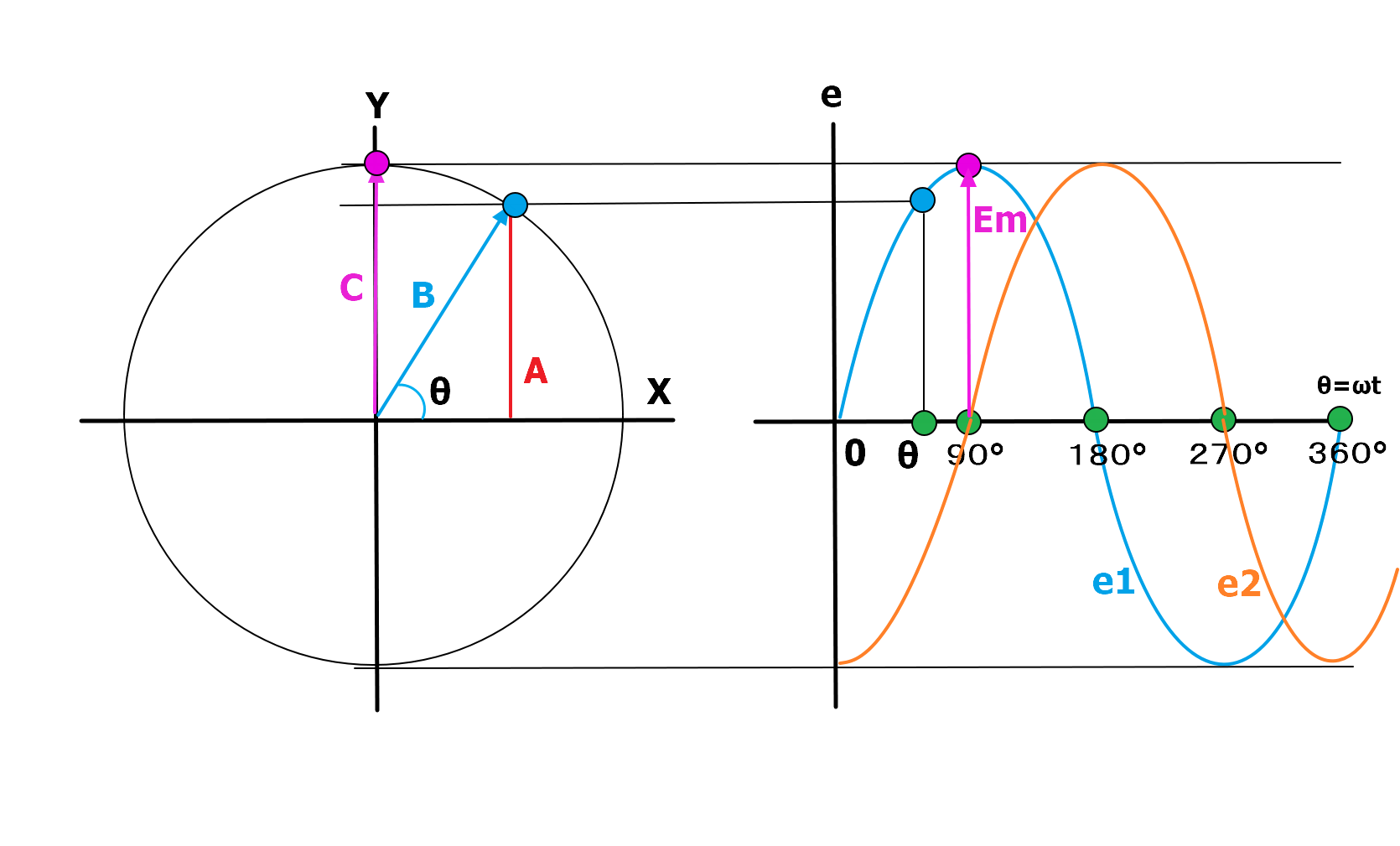
正弦波交流の電圧e1で位相がθの時、電圧の大きさは左のベクトルからAの大きさになるのが分かります。

大きさAはBの縦分の大きさになるため、A＝Bsinθで求められます。

そして、このBの大きさは同じ円の中にあるCの大きさと等しいのが分かります。

Cは右の波形の中で、最大値に等しいため、Eｍsinθで瞬時値を表せることになります。

また、角度θは時間の経過とともに大きくなり、角度×ｔで電圧変化のタイミングを表せます。

この角度θは角速度や角周波数と呼ばれていて、ωで表し、１秒間に角度がどれくらい変化するのかをわかるようにしたものです。

単位には度数法の[°]ではなく弧度法でラジアン[rad/s]が使用されます。

弧度法というのは扇形の弧と半径の長さの関係から角度を表す方法です。

また、角速度ωは２πｆで求めることができます。

なぜ角速度が２πｆになるのかというと、発電機にはコイルが使われており、コイルの１回転が波形の１周期となるからです。

コイルの１回転は３６０°で、３６０°を弧度法で表すと２πになります。

ｆは周波数のことであり、発電機の周波数と１秒間のコイルの回転数は等しいことから、２π×周波数（回転数）×時間で電圧変化のタイミングを表しています。

これらのことから瞬時値は下のように表されます。

$$e1=Em\sinω(2πf)t　[V]$$

一方、e2の瞬時値はe1と大きさが同じで、e1の電圧よりも位相が９０°遅れていることから、

$$e2=Em\sin(ωt-90)[V]$$

となります。

少し長くなってしまいましたが、これが交流の瞬時値、あるタイミングの時の大きさの表し方です。

正弦波交流の平均値とは

今度は正弦波交流の平均値です。

平均の電圧はVavやEav、電流であればIavなど使用します。

平均値というと真ん中の位置をイメージするので０になりそうな気がしますが、もちろん０ではありません。

０ではおかしくなってしまうため、平均値は正弦波形の半周期(瞬時値の和の平均）を平均として計算しています。

言い換えると、絶対値の平均とも言えます。

下の図でいうと、１周期の半分である山の面積を求めることがこの波形の平均値となります。

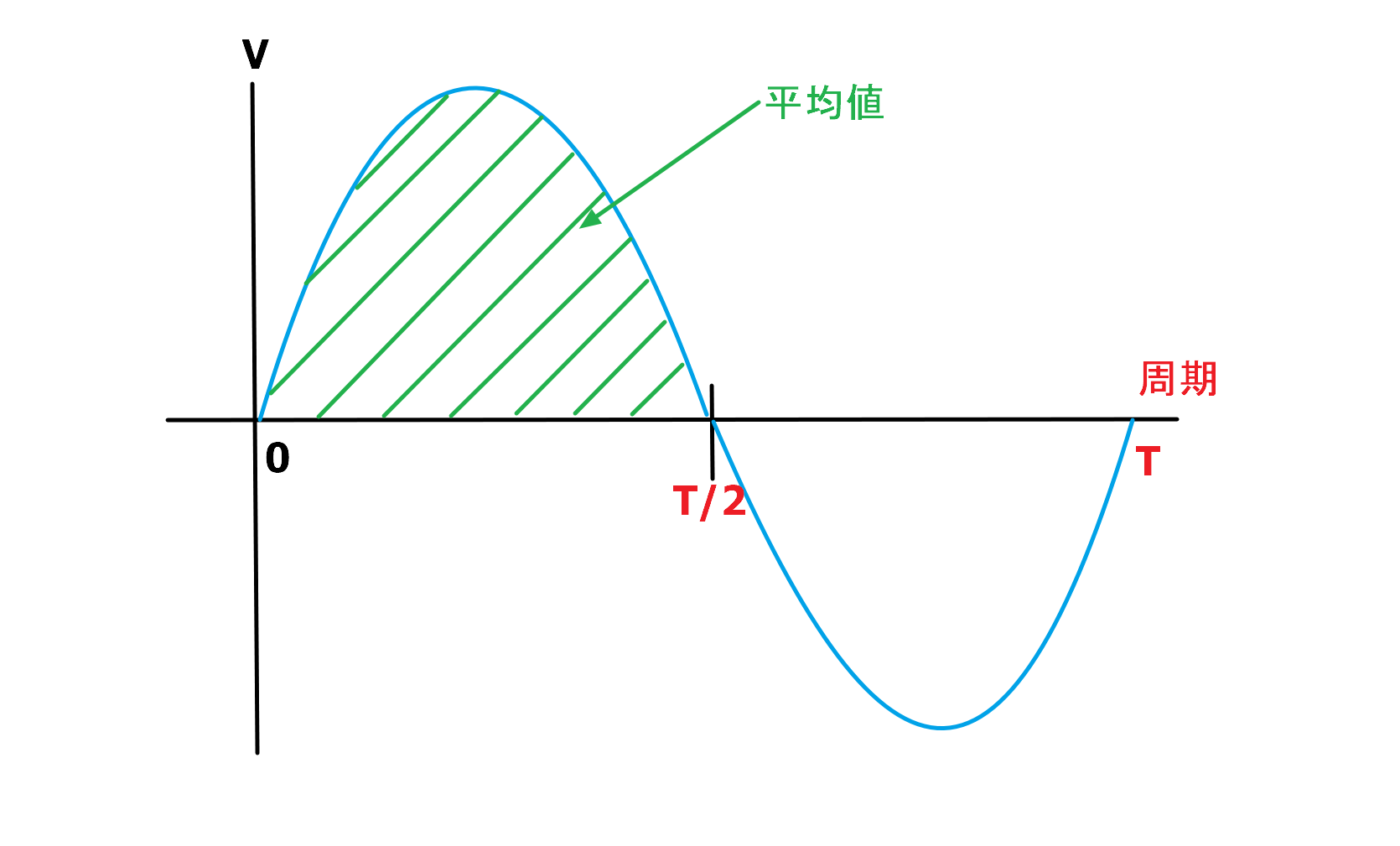
１周期をTとすると、半周期はT／２です。

半周期の山の面積を求めるためには０～T／２を積分をすると求められます。

電圧の平均を求めるため、実際に積分の式をつくり計算すると、

$$Vav=\frac{1}{T}\int_0^\frac{T}{2}Vm\sin\frac{2π}{T}tdt$$

$$=\frac{2Vm}{T}\left[-\frac{T}{2π}\cos\frac{2π}{T}t\right]_0^\frac{T}{2}$$

$$=\frac{2Vm}{T}・\frac{T}{2π}(-\cosπ+\cos0)$$

$$=\frac{Vm}{π}・2$$

$$=\frac{2}{π}Vm$$

となることから、平均値は最大値に２／πをかけたものになります。

ピークピーク値

最後はピークピーク値というものです。

正弦波形の最大値と最小値の差を表します。下の図でいうと矢印の部分になります。

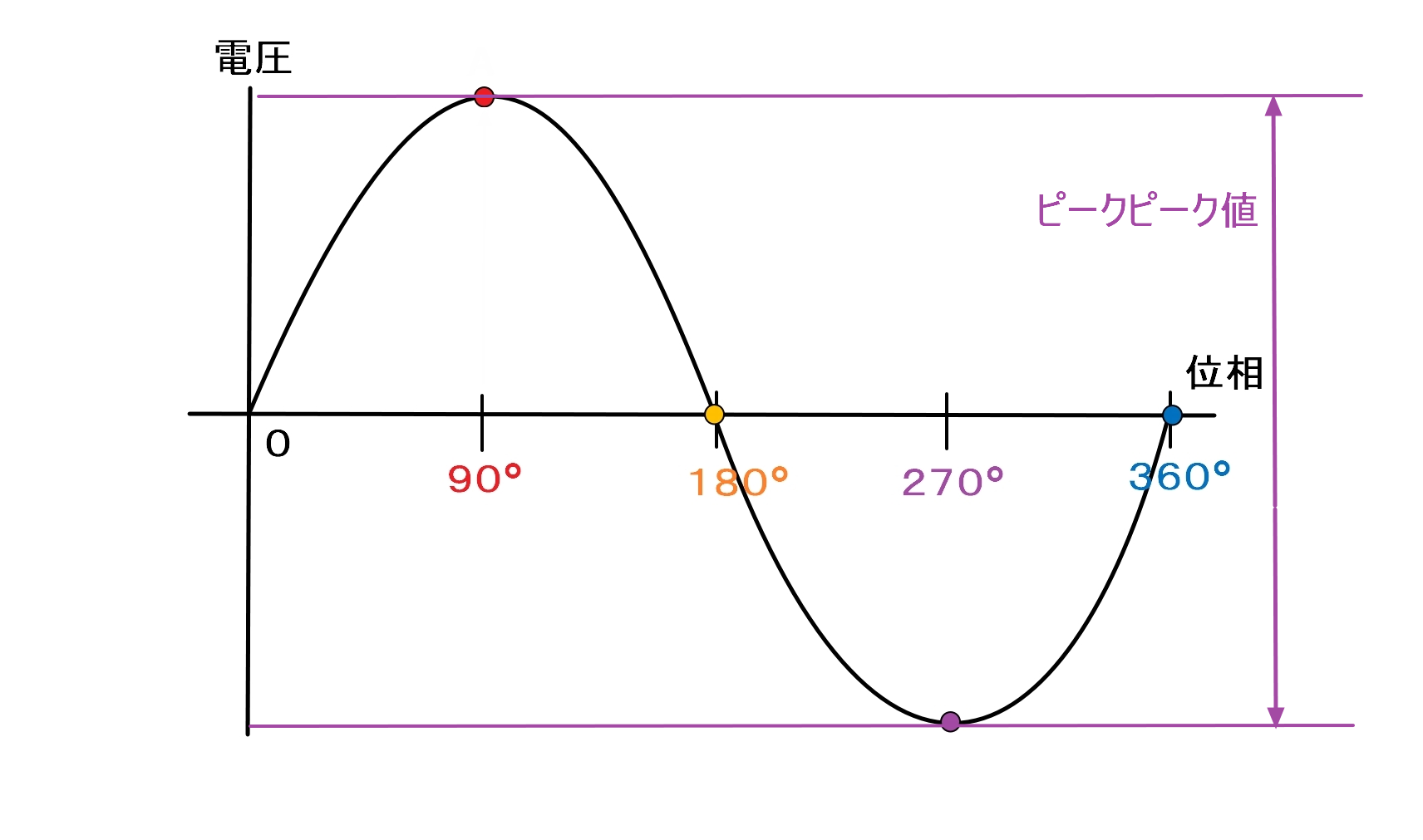
ピークピーク値の記号は電圧であればＥｐｐやＶｐｐ、電流であればＩｐｐが使用されます。

まとめ

以上が正弦波交流の大きさの表し方をまとめたものです。

このように交流の電気には大きさが常に変化する性質があることから、様々な表し方があります。

また、正弦波交流には位相というものがあり、位相のことを理解していないと何も理解することができません。

下の記事では正弦波交流の位相とはどんなものなのか詳しく解説していますので、是非合わせて読んでみてください。

【５分でわかる！】交流の電気の位相差とは何か？わかりやすく解説